Question

The triangle ABC is defined by the vertices $A\left( 1,-2,2 \right),B\left( 1,4,0 \right)$ and $C\left( -4,1,1 \right)$ If $M$ be the foot of the altitude drawn from the vertex B to side AC, then $\overrightarrow{BM}=$ \[\]
A. $\left( \dfrac{-20}{7},\dfrac{-30}{7},\dfrac{10}{7} \right)$\[\]
B.$\left( -20,-30,10 \right)$\[\]
C.$\left( 2,3,-1 \right)$\[\]
D.$\left( 1,2,3 \right)$\[\]

Answer 1

Hint: We know that the ray from point $P\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)$ and $Q\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$ can be represented as the vector $\overrightarrow{PQ}=\left( {{x}_{2}}-{{x}_{1}} \right)\hat{i}+\left( {{y}_{2}}-{{y}_{1}} \right)\hat{j}+\left( {{z}_{2}}-{{z}_{1}} \right)\hat{k}$. We represent the sides as the vectors$\overrightarrow{AB},\overrightarrow{BC},\overrightarrow{CA}$. We find position vector point on the line as $\overrightarrow{a}+\lambda \overrightarrow{d}$ where $\overrightarrow{a}$ vector is the potion vector of vertex C and $\overrightarrow{d}=\overrightarrow{CA}$ as the direction vector. We use the perpendicular condition of vectors $\overrightarrow{BM}$ and $\overrightarrow{CA}$ to find $\lambda $. \[\]

Complete step-by-step solution:’

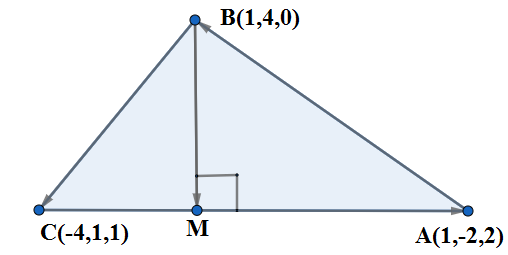
We are given the coordinate of the vertices $A\left( 1,-2,2 \right),B\left( 1,4,0 \right)$ and $C\left( -4,1,1 \right)$. Let us represent the sides as vectors. We have;
\[\begin{align}
  & \overrightarrow{AB}=\left( 1-1 \right)\hat{i}+\left( 4-\left( -2 \right) \right)\hat{j}+\left( 0-\left( 2 \right) \right)\hat{k}=6\hat{j} -2\hat{k} \\
 & \overrightarrow{BC}=\left( -4-1 \right)\hat{i}+\left( 1-4 \right)\hat{j}+\left( 1-\left( 0 \right) \right)\hat{k}=-5\hat{j}-3\hat{j}+1 \hat{k} \\
 & \overrightarrow{CA}=\left( 1-\left( -4 \right) \right)\hat{i}+\left( -2-1 \right)\hat{j}+\left( 2-1 \right)\hat{k}=5\hat{i}-3\hat{j}+\hat{k} \\
\end{align}\]
We know that vector equation of given by $\overrightarrow{a}+\lambda \overrightarrow{d}$ where $\overrightarrow{a}$ is position vector of any point on the line and $\overrightarrow{d}$ is the direction parallel vector to the line. The vector $\overrightarrow{a}+\lambda \overrightarrow{d}$ is also the position vector of all points on the line.
Let us observe the given triangle ABC. The position vector of vertex C is $\overrightarrow{a}=-4\hat{i}+\hat{j}+\hat{k}$ and the direction vector from point C is $\overrightarrow{CA}$ that is $\overrightarrow{d}=\overrightarrow{CA}=5\hat{i}-3\hat{j}+\hat{k}$. So the position vector any point on the line AC is
\[\begin{align}
  & \overrightarrow{a}+\lambda \overrightarrow{d}=-4\hat{i}+\hat{j}+\hat{k}+\lambda \left( 5\hat{i}-3\hat{j}+\hat{k} \right) \\
 & \Rightarrow \overrightarrow{a}+\lambda \overrightarrow{d}=\left( -4+5\lambda \right)\hat{i}+\left( 1-3\lambda \right)\hat{j}+\left( 1+\lambda \right)\hat{k} \\
\end{align}\]
We are given M is the foot of the altitude drawn from the vertex B to side AC. The above vector is also the position vector of M since M lies on line AC. So the coordinates of the point M can be represented as $M\left( -4+5\lambda ,1-3\lambda ,1+\lambda \right)$ . We can represented the given altitude BM as the vector
\[\begin{align}
  & \overrightarrow{BM}=\left( -4+5\lambda -1 \right)\hat{i}+\left( 1-3\lambda -4 \right)\hat{j}+\left( 1+\lambda \right)\hat{k} \\
 & \Rightarrow \overrightarrow{BM}=\left( -5+5\lambda \right)\hat{i}+\left( -3-3\lambda \right)\hat{j}+\left( 1+\lambda \right)\hat{k} \\
\end{align}\]
Since $\overrightarrow{BM}$and $\overrightarrow{CA}=5\hat{i}-3\hat{j}+\hat{k}$ are perpendicular to each other we have
\[\begin{align}
  & 5\left( 5\lambda - 5 \right)+-3\left( -3-3\lambda \right)+1\left( 1+\lambda \right)=0 \\
 & \Rightarrow 25\lambda -25+9+9\lambda +1+\lambda =0 \\
 & \Rightarrow 35\lambda -15=0 \\
 & \Rightarrow \lambda =\dfrac{15}{35}=\dfrac{3}{7} \\
\end{align}\]
So the required vector is
\[\begin{align}
  & \overrightarrow{BM}=\left( -5+5\cdot \dfrac{3}{7} \right)\hat{i}+\left( -3-3\cdot \dfrac{3}{7} \right)\hat{j}+\left( 1+\dfrac{3}{7} \right)\hat{k} \\
 & \Rightarrow \overrightarrow{BM}=\left( \dfrac{-20}{7} \right)\hat{i}+\left( -\dfrac{30}{7} \right)\hat{j}+\left( \dfrac{10}{7} \right)\hat{k} \\
\end{align}\]
So the correct option is A.

Note: We note that if two vectors in space are represented in component forms $\overrightarrow{a}={{a}_{1}}\hat{i}+{{a}_{2}}\hat{j}+{{a}_{3}}\hat{k}$ and $\overrightarrow{b}={{b}_{1}}\hat{i}+{{b}_{2}}\hat{j}+{{b}_{3}}\hat{k}$ then their perpendicular condition is given by ${{a}_{1}}{{b}_{1}}+{{a}_{2}}{{b}_{2}}+{{a}_{3}}{{b}_{3}}=0$. We can alternatively solve using projection. We find $\overrightarrow{BM}$ as the component of $\overrightarrow{AB}$ perpendicular to $\overrightarrow{AC}$ which $\overrightarrow{BM}=\overrightarrow{AB}-\dfrac{\left( \overrightarrow{AB}\cdot \overrightarrow{AC} \right)\overrightarrow{AC}}{{{\left( \overrightarrow{AC} \right)}^{2}}}$.