Question

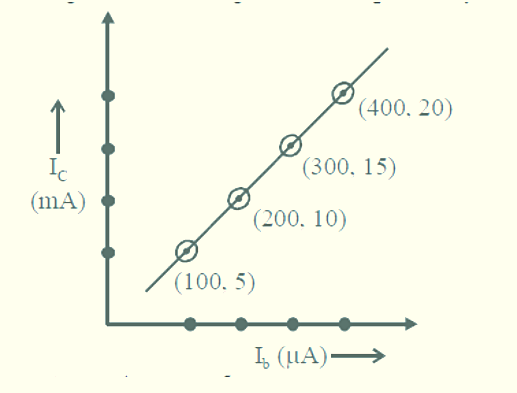
The transfer acceleration curve of a transistor, having input and output resistance 100 ohm and 100 kilo ohm respectively, is shown in figure. The voltage and power gain, are respectively:
                 

$A){\text{ 5}} \times {\text{1}}{{\text{0}}^4},{\text{ 5}} \times {\text{1}}{{\text{0}}^5} \\$
$B){\text{ 5}} \times {\text{1}}{{\text{0}}^4},{\text{ 5}} \times {\text{1}}{{\text{0}}^6} \\$
$C){\text{ 5}} \times {\text{1}}{{\text{0}}^4},{\text{ 2}}{\text{.5}} \times {\text{1}}{{\text{0}}^6} \\$
$D){\text{ 2}}{\text{.5}} \times {\text{1}}{{\text{0}}^4},{\text{ 2}}{\text{.5}} \times {\text{1}}{{\text{0}}^6} \\ $

Answer 1

Hint: The term gain, basically it is a ratio of the output magnitude to the input magnitude. It is represented by A. Its SI unit is dB (decibel). The expression:
$Gain\; = \;\dfrac{{Output}}{{Input}}$

Complete answer:
So, here the given condition is,
Output resistance is 100 kilo ohm = 100000 ohm
Input resistance is 100 ohm
So, we have to calculate the change in collector current is because it is the output current
$\Delta {I_C} = 10mA - 5mA \\$
$\Delta {I_C} = 5mA \\$
$\Delta {I_C} = 5 \times {10^{ - 3}}A \\ $
So, we have to calculate the change in base current is because it is the input current
$\Delta {I_B} = 200\mu A - 100\mu A \\$
$\Delta {I_B} = 100\mu A \\$
$\Delta {I_B} = 100 \times {10^{ - 6}}A \\ $
We have to calculate the voltage gain,
So, the voltage gain, it is the ratio of voltage out to the voltage in. It is represented by AV. The expression for this:
$Voltage\;Gain = \dfrac{{Voltage\;Out}}{{Voltage\;In}} \\$
${A_V} = \dfrac{{{V_{Out}}}}{{{V_{In}}}} \\ $
So, we can also calculate the voltage gain with the help of ohm’s law
V = IR -- (1)
So, we have to find voltage gain, so we change the expression as a gain
So, the expression is
${V_{gain}} = {I_{gain}} \times {R_{gain}} \\$
${A_V} = \dfrac{{\Delta {I_C}}}{{\Delta {I_B}}} \times \dfrac{{{R_{out}}}}{{{R_{in}}}} \\$
${A_V} = \dfrac{{5 \times {{10}^{ - 3}}}}{{100 \times {{10}^{ - 6}}}} \times \dfrac{{100000}}{{100}} \\$
${A_V} = \;\dfrac{{5 \times {{10}^2}}}{{100 \times {{10}^{ - 4}}}} \\$
${A_V} = 5 \times {10^2} \times {10^2} \\$
${A_V} = 5 \times {10^4} \\ $
We have to calculate the power gain,
So, the power gain, it is the ratio of power out to the power in. It is represented by AP. The expression for this:
$Power\;Gain = \dfrac{{Power\;Out}}{{Power\;In}} \\$
${A_P} = \dfrac{{{P_{Out}}}}{{{P_{In}}}} \\ $
So, we can also calculate the power gain with the help of the expression of the power dissipation in terms of current and the voltage
$Power = Voltage \times Current$
So, we have to find power gain, so we change the expression as a gain
So, the expression is
${P_{gain}} = {V_{gain}} \times {I_{gain}} \\$
${A_P} = {A_V} \times \dfrac{{\Delta {I_C}}}{{\Delta {I_B}}} \\$
${A_P} = 5 \times {10^4} \times \dfrac{{5 \times {{10}^{ - 3}}}}{{100 \times {{10}^{ - 6}}}} \\$
${A_P} = \dfrac{{25 \times {{10}^{ - 1}}}}{{100 \times {{10}^{ - 6}}}} \\$
${A_P} = 25 \times {10^5} \\ $
So, the voltage gain is $5 \times {10^4}$ and, the power gain is $25 \times {10^5}$ we can also write as $2.5 \times {10^6}$

So, the option (C) is correct.

Note:
Here, the current gain, it is the ratio of current out to the current in. It is represented by AI. The expression for this:
$Current\;Gain = \dfrac{{Current\;Out}}{{Current\;In}} \\$
${A_I} = \dfrac{{{I_{Out}}}}{{{I_{In}}}} \\ $
Here, the resistance gain, it is the ratio of resistance out to the resistance in. It is represented by AR. The expression for this:
$\operatorname{Resistance}\;Gain = \dfrac{{\operatorname{Resitan ce}\;Out}}{{\operatorname{Resistance}\;In}} \\$
${A_R} = \dfrac{{{R_{Out}}}}{{{R_{In}}}} \\ $
We can also calculate the power in terms of resistance and current as well as in terms of voltage and resistance because we have an expression of power dissipation.