Question

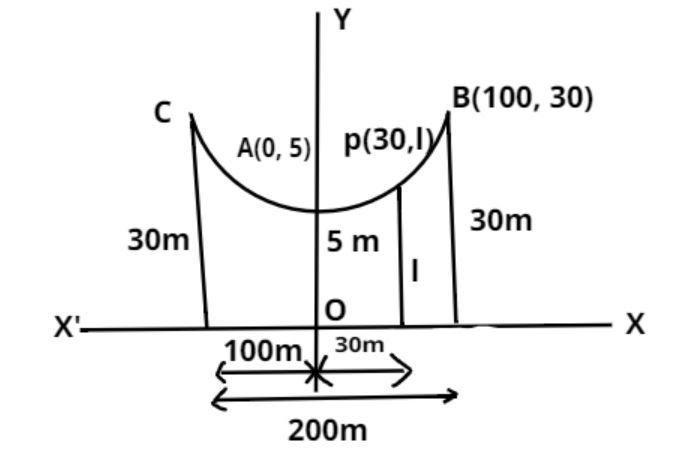
The tower of a bridge, hung in the form of a parabola, has their tops 30m above the roadway and is 200 meters apart. If the cable is 5m above the roadway at the centre of the bridge, find the length of the vertically supporting cable 30m from the centre.

Answer 1

Hint: Here we have to find the length of the vertically supporting cable taking the coordinates and equating to the equation of parabola.

Complete step-by-step answer:
Let CAB be the bridge and X`OX be the roadway. Let A be the centre of the bridge.
Taking X`OX as x-axis and y-axis along OA, we find that the coordinates of A are (0, 5). Clearly the bridge is in the shape of a parabola having its vertex at A (0, 5). Let its equation be
${x^2} = 4a\left( {y - 5} \right)..........(1)$
It passes through B (100, 30)
$ \Rightarrow {100^2} = 4a\left( {30 - 5} \right)$
$ \Rightarrow a = 100$
Putting the value of a in equation 1, we get
${x^2} = 400\left( {y - 5} \right)..........(2)$
Let ‘l’ meters be the length of a vertical supporting cable 30 meter from the centre. Then, P(30,l) lies on equation 2.
$ \Rightarrow 900 = 400\left( {l - 5} \right)$
$ \Rightarrow l = \dfrac{9}{4} + 5 = \dfrac{{29}}{4}m$
Hence the length of vertical supporting cable 30m from the centre of the bridge is $\dfrac{{29}}{4}m$ .

Note: In this type of problem first assume the vertically upward parabola then mark the points according to given condition, then satisfy these points in the equation of parabola, you will get your answer.