Question

The total tangential and normal accelerations of the balloon.

Answer 1

Hint: The balloon is rising upwards as well as it is moving horizontally. First we need to consider the individual velocities i.e. along the vertical a constant and along the horizontal a function of y. Hence further obtaining the components of acceleration along the y and x direction will enable us to determine the total, normal and the tangential acceleration of the balloon.
Formula used:
$V=\sqrt{{{\left( {{V}_{x}} \right)}^{2}}+{{\left( {{V}_{y}} \right)}^{2}}}$

Complete answer:

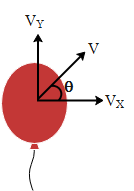
From the above diagram we can see that the balloon has a component of velocity along the vertical as well as the horizontal. Let the velocity along the vertical be a constant i.e. ${{V}_{y}}={{V}_{\circ }}$ and the velocity along the horizontal be a function of y i.e.${{V}_{x}}=ky$ . Hence the resultant of the velocity (V) using laws of vector addition we get,
$\begin{align}
  & V=\sqrt{{{\left( {{V}_{x}} \right)}^{2}}+{{\left( {{V}_{y}} \right)}^{2}}} \\
 & \Rightarrow V=\sqrt{{{\left( ky \right)}^{2}}+{{\left( {{V}_{o}} \right)}^{2}}} \\
\end{align}$
The acceleration of a particle is defined as the rate of change of speed with respect to time. Hence using the laws of vector addition, if ${{a}_{x}}$ is the component of acceleration along x direction and ${{a}_{y}}$ is the component along y direction than the total acceleration (${{a}_{T}}$) is,
$\begin{align}
  & {{a}_{T}}=\sqrt{{{\left( {{a}_{x}} \right)}^{2}}+{{\left( {{a}_{y}} \right)}^{2}}} \\
 & \because {{a}_{y}}=\dfrac{d{{V}_{\circ }}}{dt}=0,\text{ }{{a}_{x}}=\dfrac{d(ky)}{dt}=k\dfrac{dy}{dt}=k{{V}_{\circ }} \\
 & {{a}_{T}}=\sqrt{{{\left( k{{V}_{\circ }} \right)}^{2}}+{{\left( 0 \right)}^{2}}} \\
 & \therefore {{a}_{T}}=\sqrt{{{\left( k{{V}_{\circ }} \right)}^{2}}}=k{{V}_{\circ }} \\
\end{align}$
From the above expression it can be interpreted that the acceleration is clearly in the x direction. Let us say the angle between ‘V’ and ${{V}_{x}}$ is $\theta $ .The component of acceleration in the direction of ‘V’ is the tangential acceleration i.e. acceleration in the direction of motion. Hence the tangential acceleration ${{a}_{t}}$ is,
$\begin{align}
  & {{a}_{t}}={{a}_{T}}\cos \theta \\
 & \because \cos \theta =\dfrac{{{V}_{x}}}{V}=\dfrac{ky}{\sqrt{{{\left( ky \right)}^{2}}+{{\left( {{V}_{o}} \right)}^{2}}}} \\
 & \Rightarrow {{a}_{t}}=k{{V}_{\circ }}\dfrac{ky}{\sqrt{{{\left( ky \right)}^{2}}+{{\left( {{V}_{o}} \right)}^{2}}}} \\
 & \therefore {{a}_{t}}=\dfrac{{{k}^{2}}y{{V}_{\circ }}}{\sqrt{{{\left( ky \right)}^{2}}+{{\left( {{V}_{o}} \right)}^{2}}}} \\
\end{align}$
Similarly, the normal component of acceleration ${{a}_{N}}$ is,
$\begin{align}
  & {{a}_{N}}={{a}_{T}}\sin \theta \\
 & \because \sin \theta =\dfrac{{{V}_{y}}}{V}=\dfrac{{{V}_{\circ }}}{\sqrt{{{\left( ky \right)}^{2}}+{{\left( {{V}_{o}} \right)}^{2}}}} \\
 & \Rightarrow {{a}_{N}}=k{{V}_{\circ }}\dfrac{{{V}_{\circ }}}{\sqrt{{{\left( ky \right)}^{2}}+{{\left( {{V}_{o}} \right)}^{2}}}} \\
 & \therefore {{a}_{N}}=\dfrac{k{{V}_{\circ }}^{2}}{\sqrt{{{\left( ky \right)}^{2}}+{{\left( {{V}_{o}} \right)}^{2}}}} \\
\end{align}$
Therefore the total acceleration is $k{{V}_{\circ }}$, tangential acceleration is $\dfrac{{{k}^{2}}y{{V}_{\circ }}}{\sqrt{{{\left( ky \right)}^{2}}+{{\left( {{V}_{o}} \right)}^{2}}}}$ and normal component of acceleration is $\dfrac{k{{V}_{\circ }}^{2}}{\sqrt{{{\left( ky \right)}^{2}}+{{\left( {{V}_{o}} \right)}^{2}}}}$

Note:
It is to be noted that the normal component of acceleration is not in the y direction. It is in the downward direction making an angle theta with the horizontal component of velocity. If there was a component of acceleration along the y direction, then the balloon would have had the acceleration vertically as well. Hence we took the velocity as a function of y in horizontal.