The total surface area of a cube is 54\[c{{m}^{2}}\]. What is the length of its side?
Answer
Verified360k+ views
Hint:Cube has 6 faces,the total surface area of the cube is given.Find out the area of one face of the cube and next length of its side.
“Complete step-by-step answer:”
Given that the total surface area of the cube = 54\[c{{m}^{2}}\].
The surface area of a cube is \[6{{a}^{2}}\].
Where, a is the length of the side of each edge of the cube.
All the sides of the cube are equal.
\[\therefore \]a is the length of one side of the cube.
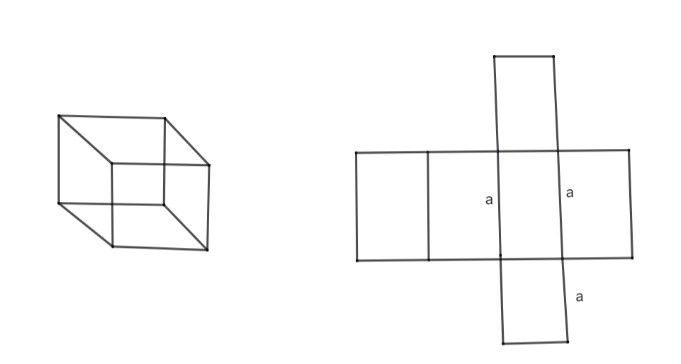
By looking at the figure, cube has six sides and each side is a square.
Length of the edge is a
\[\therefore \]Area of a square\[=a\times a={{a}^{2}}\]
Since, there are six sides, the total surface area is
Surface area\[={{a}^{2}}+{{a}^{2}}+{{a}^{2}}+{{a}^{2}}+{{a}^{2}}+{{a}^{2}}=6{{a}^{2}}\]
\[\therefore \]Surface area of cube is = \[6{{a}^{2}}\]
We have given the total surface area of cube = 54\[c{{m}^{2}}\].
\[\begin{align}
& \Rightarrow 6{{a}^{2}}=54 \\
& \therefore {{a}^{2}}=\dfrac{54}{6} \\
& \Rightarrow {{a}^{2}}=9 \\
& \therefore a=\sqrt{9}=3 \\
\end{align}\]
Length of its side = 3cm
Note: Cube has 6 faces, so the total surface area becomes \[6{{a}^{2}}\].
“Complete step-by-step answer:”
Given that the total surface area of the cube = 54\[c{{m}^{2}}\].
The surface area of a cube is \[6{{a}^{2}}\].
Where, a is the length of the side of each edge of the cube.
All the sides of the cube are equal.
\[\therefore \]a is the length of one side of the cube.
By looking at the figure, cube has six sides and each side is a square.
Length of the edge is a
\[\therefore \]Area of a square\[=a\times a={{a}^{2}}\]
Since, there are six sides, the total surface area is
Surface area\[={{a}^{2}}+{{a}^{2}}+{{a}^{2}}+{{a}^{2}}+{{a}^{2}}+{{a}^{2}}=6{{a}^{2}}\]
\[\therefore \]Surface area of cube is = \[6{{a}^{2}}\]
We have given the total surface area of cube = 54\[c{{m}^{2}}\].
\[\begin{align}
& \Rightarrow 6{{a}^{2}}=54 \\
& \therefore {{a}^{2}}=\dfrac{54}{6} \\
& \Rightarrow {{a}^{2}}=9 \\
& \therefore a=\sqrt{9}=3 \\
\end{align}\]
Length of its side = 3cm
Note: Cube has 6 faces, so the total surface area becomes \[6{{a}^{2}}\].
Last updated date: 18th Sep 2023
•
Total views: 360k
•
Views today: 3.60k
