Question

The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of ${{30}^{0}}$ with horizontal, then the length of the wire is.
(a) 12 m
(b) 10 m
(c) 8 m
(d) 6 m

Answer 1

Hint: For solving this problem first we will draw the geometrical figure as per the given data. After that, we will use the basic formula of trigonometry $\sin \theta =\dfrac{\left( \text{length of the perpendicular} \right)}{\left( \text{length of the hypotenuse} \right)}$ and solve correctly to get the length of the wire easily.

Complete step-by-step answer:
Given:
 It is given that the tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of ${{30}^{0}}$ horizontally and we have to find the length of the wire.
Now, first, we will draw a geometrical figure as per the given data. For more clarity look at the figure given below:

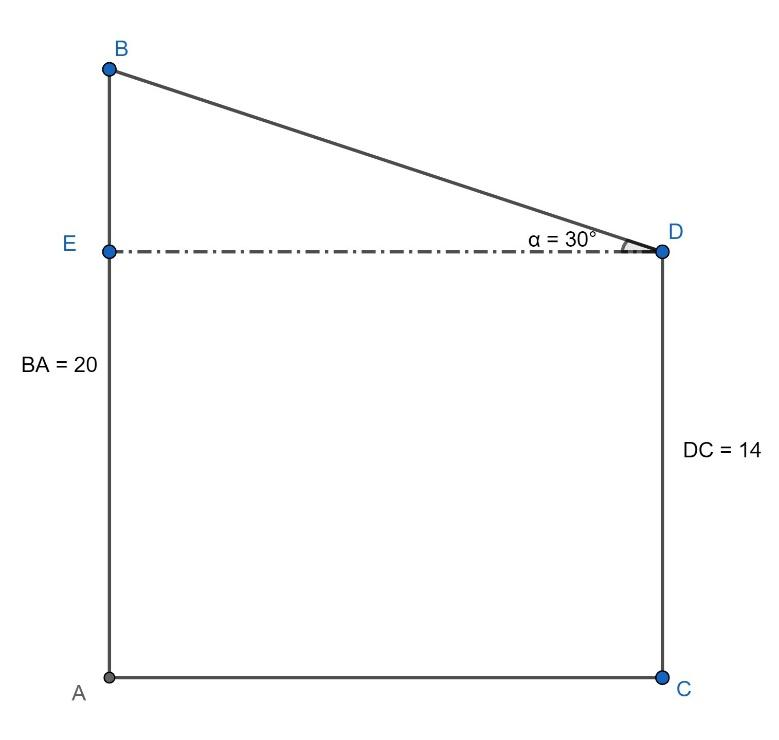
In the above figure BA is the pole of length 20 m, DC is the pole of length 14 m, BD is equal to the length of the wire and ED is the horizontal line so, as per the given data $\angle BDE={{30}^{0}}$ .
Now, as BA and DC are vertical as the poles will be standing vertical to the ground so, length EA will be equal to the length of the DC. Then,
$\begin{align}
  & BA=BE+EA \\
 & \Rightarrow BE=BA-EA \\
 & \Rightarrow BE=BA-DC \\
\end{align}$
Now, put the value of BA = 20 m and DC = 14 m in the above equation. Then,
$\begin{align}
  & BE=BA-DC \\
 & \Rightarrow BE=20-14 \\
 & \Rightarrow BE=6\text{ m} \\
\end{align}$
Now, from the above result, we can write that the length of BE will be 6 m.
Now, we consider $\Delta BDE$ in which $\angle BED={{90}^{0}}$ , $\angle BDE={{30}^{0}}$ and $BE=6\text{ m}$ . Then,
$\begin{align}
  & \sin \left( \angle BDE \right)=\dfrac{\left( \text{length of the perpendicular BE} \right)}{\left( \text{length of the hypotenuse BD} \right)} \\
 & \Rightarrow \sin {{30}^{0}}=\dfrac{BE}{BD} \\
 & \Rightarrow 0.5=\dfrac{6}{BD} \\
 & \Rightarrow BD=12\text{ m} \\
\end{align}$
Now, from the above result, we conclude that the length of BD will be 12 m.
Thus, the length of the wire will be 12 m.
Hence, (a) is the correct option.


Note: Here, the student should first try to understand what is asked in the problem. After that, we should try to draw the geometrical figure as per the given data. Moreover, we should apply the basic formula of trigonometry properly without any error and avoid calculation mistakes while solving to get the correct answer.