Question

The time taken by a body to slide down a rough 45$^\circ $ incline plane is twice that required to slide down a smooth 45$^\circ $ incline plane. The coefficient of kinetic friction between the object and rough plane is given by
$
  {\text{A}}{\text{. }}\dfrac{1}{3} \\
  {\text{B}}{\text{. }}\dfrac{3}{4} \\
  {\text{C}}{\text{. }}\sqrt {\dfrac{3}{4}} \\
  {\text{D}}{\text{. }}\sqrt {\dfrac{4}{3}} \\
 $

Answer 1

Hint: The rough inclined plane will offer friction to the body sliding down it while the smooth inclined plane will not offer any friction to the body sliding down it. By drawing a free body diagram and solving the obtained equations of motion for two cases, we can get the required value of coefficient of friction.

Complete step-by-step answer:
Let us first consider a rough inclined plane which is inclined at an angle of 45$^\circ $. The following free body diagram shows the forces which will act on a body sliding down such an inclined plane.

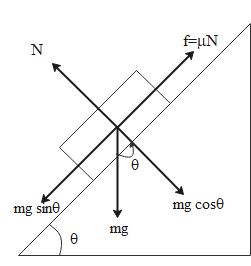
The net downward force acting on the body which results in sliding of the body is equal to the difference between the downward force along the surface and the friction force acting in the opposite direction along the surface. Therefore, using Newton’s second law of motion,
$
  ma = mg\sin \theta - \mu mg\cos \theta \\
  \Rightarrow a = g\sin 45^\circ - \mu g\cos 45^\circ \\
  \Rightarrow a = \dfrac{{\left( {1 - \mu } \right)g}}{{\sqrt 2 }} \\
 $
Now the time taken to slide down this rough inclined plane can be calculated by using the second equation of motion in the following way. The initial velocity of the body is zero since it starts sliding from rest.
$
  S = ut + \dfrac{1}{2}a{t^2} \\
 \Rightarrow S = 0 + \dfrac{1}{2} \times \dfrac{{\left( {1 - \mu } \right)g}}{{\sqrt 2 }} \times t_1^2 \\
 \Rightarrow S = \dfrac{{\left( {1 - \mu } \right)g}}{{2\sqrt 2 }} \times t_1^2 \\
 $
Here ${t_1}$ is the time taken by the body to slide down this rough inclined plane.
Now in case of the smooth inclined plane, there will be no friction force acting on the body, so we can write the above expression for acceleration for the smooth inclined plane in the following way.
$a = \dfrac{g}{{\sqrt 2 }}$
Similarly, the distance travelled by body down the smooth inclined plane can be written as
$
  S = 0 + \dfrac{1}{2} \times \dfrac{g}{{\sqrt 2 }} \times t_2^2 \\
 \Rightarrow S = \dfrac{g}{{2\sqrt 2 }} \times t_2^2 \\
 $
Here ${t_2}$ is the time taken by the body to slide down this smooth inclined plane and according to the given condition.
${t_1} = 2{t_2}$
Also, the body will be sliding down through the same distance, therefore, we have
$
  \dfrac{{\left( {1 - \mu } \right)g}}{{2\sqrt 2 }} \times t_1^2 = \dfrac{g}{{2\sqrt 2 }} \times t_2^2 \\
\Rightarrow \left( {1 - \mu } \right)t_1^2 = t_2^2 \\
 \Rightarrow \left( {1 - \mu } \right)4t_2^2 = t_2^2 \\
\Rightarrow 1 - \mu = \dfrac{1}{4} \\
\Rightarrow \mu = 1 - \dfrac{1}{4} \\
  \Rightarrow \mu = \dfrac{3}{4} \\
 $
This is the required answer. Hence, the correct answer is option B.

So, the correct answer is “Option B”.

Note: It should be noted that since friction offers resistance to the motion of an object, the body takes longer time to slide down the rough inclined plane than the smooth inclined plane. In case of a smooth incline plane, there is no opposite motion acting on the body and it slides down freely due to its weight only.