Question

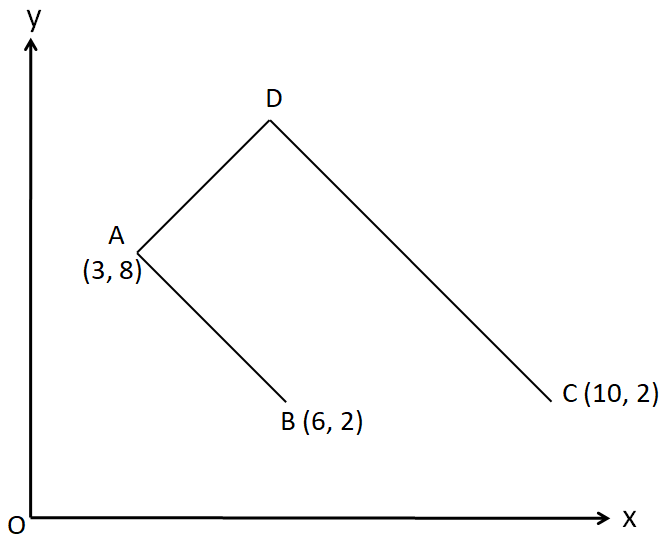
The three points $A\left( 3,8 \right)$, $B\left( 6,2 \right)$ and $C\left( 10,2 \right)$ are shown in the diagram. The point D is such that the line DA is perpendicular to AB and DC is parallel to AB. Calculate the coordinates of D.

Answer 1

Hint: Since the coordinates of the points A and B are given, we can determine the slope of the line AB, using the formula $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$. Since the line DC is given parallel to AB, its slope will be equal to that of AB. And since AD is given to be perpendicular to AB, the product of the slope of AB and AD will be equal to $-1$, from which the slope of AD can be determined. Finally, using the point-slope form, we can determine the equations for the lines AD and DC, and on solving them for x and y, we will get the required coordinates for the point D.

Complete step-by-step answer:
We know that the slope of a line passing through two points having coordinates $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is given by
$\Rightarrow m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
Now, the coordinates of the points A and B are respectively $\left( 3,8 \right)$ and $\left( 6,2 \right)$. Therefore, the slope of the line AB is given as
\[\begin{align}
  & \Rightarrow {{m}_{AB}}=\dfrac{2-8}{6-3} \\
 & \Rightarrow {{m}_{AB}}=\dfrac{-6}{3} \\
 & \Rightarrow {{m}_{AB}}=-2........\left( i \right) \\
\end{align}\]
Now, according to the question the line DC is parallel to AB. Therefore, its slope must be equal to that of AB, which means
$\Rightarrow {{m}_{DC}}={{m}_{AB}}$
Substituting (i) we get
$\Rightarrow {{m}_{DC}}=-2......\left( ii \right)$
Also, the line DA is perpendicular to AB. SO the slope of DA can be given as
$\Rightarrow {{m}_{DA}}{{m}_{AB}}=-1$
Substituting (i) we get
$\begin{align}
  & \Rightarrow {{m}_{DA}}\left( -2 \right)=-1 \\
 & \Rightarrow {{m}_{DA}}=\dfrac{1}{2}........\left( iii \right) \\
\end{align}$
Now, the coordinates of the point C are $\left( 10,2 \right)$. Therefore, using the point slope form we can write the equation of the line CD as
$\Rightarrow \left( y-2 \right)={{m}_{DC}}\left( x-10 \right)$
Substituting (ii) we get
\[\begin{align}
  & \Rightarrow \left( y-2 \right)=\left( -2 \right)\left( x-10 \right) \\
 & \Rightarrow y-2=-2x+20 \\
\end{align}\]
Adding \[2\] both sides, we get
$\begin{align}
  & \Rightarrow y-2+2=-2x+20+2 \\
 & \Rightarrow y=-2x+22.......\left( iv \right) \\
\end{align}$
Similarly, we can write the equation of the line DA as
$\Rightarrow y-8={{m}_{DA}}\left( x-3 \right)$
Substituting (iii) we get
$\Rightarrow y-8=\dfrac{1}{2}\left( x-3 \right)$
Multiplying by $2$ both the sides we get
$\begin{align}
  & \Rightarrow 2\left( y-8 \right)=2\left( \dfrac{1}{2} \right)\left( x-3 \right) \\
 & \Rightarrow 2y-16=x-3 \\
\end{align}$
Adding $16$ both the sides we get
$\begin{align}
  & \Rightarrow 2y-16+16=x-3+16 \\
 & \Rightarrow 2y=x+13.....\left( v \right) \\
\end{align}$
Now, the lines DA and DC intersect at the point D. Therefore, to get the coordinates of the point D, we have to solve the equation (iv) and (v). For this, we put the equation (iv) in (v) to get
$\begin{align}
  & \Rightarrow 2\left( -2x+22 \right)=x+13 \\
 & \Rightarrow -4x+44=x+13 \\
\end{align}$
Adding $4x$ both sides
\[\begin{align}
  & \Rightarrow -4x+44+4x=x+13+4x \\
 & \Rightarrow 44=5x+13 \\
 & \Rightarrow 5x+13=44 \\
\end{align}\]
Subtracting \[13\] from both the sides we get
\[\begin{align}
  & \Rightarrow 5x+13-13=44-13 \\
 & \Rightarrow 5x=31 \\
\end{align}\]
Dividing both sides by \[5\]
$\begin{align}
  & \Rightarrow \dfrac{5x}{5}=\dfrac{31}{5} \\
 & \Rightarrow x=6.2 \\
\end{align}$
Putting this in the equation (iv) we get
\[\begin{align}
  & \Rightarrow y=-2\left( 6.2 \right)+22 \\
 & \Rightarrow y=-12.4+22 \\
 & \Rightarrow y=9.6 \\
\end{align}\]
Hence, the coordinates of the point D are $\left( 6.2,9.6 \right)$.

Note: We must remember the different forms of equations of a straight line such as the two point form, slope intercept form etc. In the above solution, we have used the substitution method to solve the two equations for obtaining the coordinates of the point D. We can use any other method such as elimination method, or the cross multiplication method.