Question

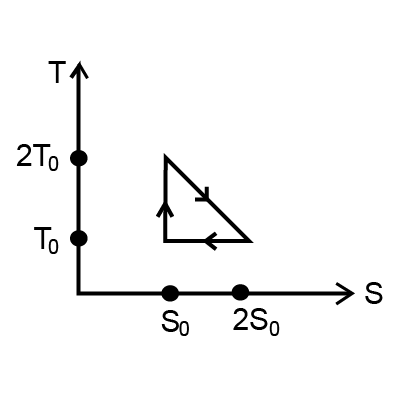
The temperature-entropy diagram of a reversible engine cycle is given in the figure. Find out Its efficiency.
(A) $\dfrac{1}{2}$
(D) $\dfrac{1}{4}$
(C) $\dfrac{1}{3}$
(D) $\dfrac{2}{3}$

Answer 1

Hint
According to the Carnot theorem, the reversible engine will always have a greater efficiency than the irreversible one. The reversible heat engine operates on a reverse cycle and functions as a heat pump (or refrigerator). The Carnot cycle is reversible representing the upper limit on the efficiency of an engine cycle.

Complete step by step answer
According to the picture,

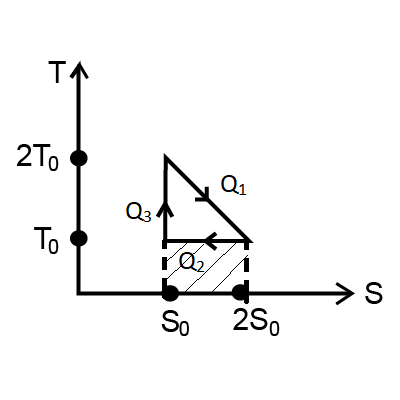
Area under S-T is equals to heat absorb or lose, Q
Now, heat from area of Q1 is = $\dfrac{1}{2} \times {T_0}{S_0} + {T_0}{S_0}$ … (1)
${Q_2} = {T_0}{S_0}$ … (2)
And, ${Q_3} = 0$ … because there is no area required for $Q_3$.
Now, The efficiency, $\eta = 1 - \dfrac{{{Q_2}}}{{{Q_1}}}$
$ \Rightarrow \eta = 1 - \dfrac{{{T_0}{S_0}}}{{\dfrac{3}{2}{T_0}{S_0}}} $
$ \Rightarrow \eta = 1 - \dfrac{2}{3} $
So, the efficiency ,$\eta = \dfrac{1}{3}$.
Option (C) is correct.

Note
Efficiency signifies a peak level of performance that uses the least amount of inputs to achieve the highest amount of output. Efficiency requires reducing the number of unnecessary resources used to produce a given output including personal time and energy.