Question

The tangents at three points A,B,C on the parabola \[{y^2} = 4x\] ,taken in pairs intersect at the points P,Q and R. If \[\Delta ,\Delta '\] be the areas of the triangles ABC and PQR respectively, then
a. \[\Delta = \Delta '\]
b. \[2\Delta ' = \Delta \]
c. \[2\Delta = \Delta '\]
d. none of these

Answer 1

Hint: We have three points given of the parabola where we will be considering the general terms of parameterization. Then we will be using the formula of the tangent on a point of the parabola. Then finding the intersection points will give us the coordinates of the vertices of the other triangle. Then using the formula of the area of the triangle we get our desired result.

Complete step by step solution:

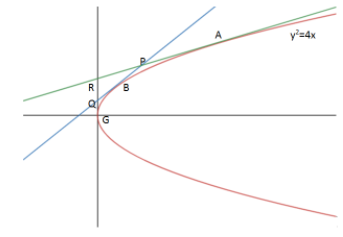
We are given three points A, B, C on the parabola \[{y^2} = 4x\] ,
Any general points on the parabola is denoted by, \[(a{t^2},2at)\] where \[a = 1\] comes from \[{y^2} = 4x\] , and t is the parameter.
So, we can denote A, B, C as, \[({t_i}^2,2{t_i})\] where, \[i = 1,2,3\] respectively.
Now, as we know, The tangents at A and B are \[{t_1}y = x + t_1^2\] ……(i)
and \[{t_2}y = x + t_2^2\] …….(ii)
Now, again, (i) – (ii) gives us,
 \[ \Rightarrow \]\[{t_1}y - {t_2}y = t_1^2 - t_2^2\]
On taking y common we get,
 \[ \Rightarrow ({t_1} - {t_2})y = t_1^2 - t_2^2\]
On cross multiplication we get,
 \[ \Rightarrow y = \dfrac{{t_1^2 - t_2^2}}{{{t_1} - {t_2}}}\]
Now as \[{a^2} - {b^2} = (a + b)(a - b)\] , we get,
 \[ \Rightarrow y = \dfrac{{({t_1} - {t_2})({t_1} + {t_2})}}{{{t_1} - {t_2}}}\]
On cancelling common terms we get,
 \[ \Rightarrow y = {t_1} + {t_2}\]
Now substituting the value of y in equation (i), we get,
 \[ \Rightarrow \] \[{t_1}({t_1} + {t_2}) = x + t_1^2\]
On expanding we get,
 \[ \Rightarrow {t_1}^2 + {t_1}{t_2} = x + t_1^2\]
On simplification we get,
 \[ \Rightarrow x = {t_1}{t_2}\]
So, two tangents intersect at, \[x = {t_1}{t_2},y = {t_1} + {t_2}\]
Then the coordinates of the vertices of P, Q, R are, \[({t_1}{t_2},{t_1} + {t_2})\] , \[({t_2}{t_3},{t_2} + {t_3})\] , \[({t_1}{t_3},{t_1} + {t_3})\]respectively
The area of the triangle ABC, \[\left| {({t_1} - {t_2})({t_2} - {t_3})({t_3} - {t_1})} \right|\]
And now, the area of the triangle PQR, \[\Delta ' = \left| {\dfrac{1}{2}\left|
  \begin{array}{*{20}{c}}
  {{t_1}{t_2}}&{{t_1} + {t_2}}&1
\end{array} \\
  \begin{array}{*{20}{c}}
  {{t_2}{t_3}}&{{t_2} + {t_3}}&1
\end{array} \\
  {t_3}{t_1}\begin{array}{*{20}{c}}
  {}&{{t_3} + {t_1}}&1
\end{array} \\
  \right|} \right|\]
If we subtract row 1 from row 2 and row 2 from row 3, we will get,
\[ \Rightarrow \] \[\Delta ' = \left| {\dfrac{1}{2}\left|
  \begin{array}{*{20}{c}}
  {({t_1} - {t_3}){t_2}}&{{t_1} - {t_3}}&0
\end{array} \\
  \begin{array}{*{20}{c}}
  {({t_2} - {t_1}){t_3}}&{{t_2} - {t_1}}&0
\end{array} \\
  {t_3}{t_1}\,\,\,\,\,\,\,\,\,\,\,\,\begin{array}{*{20}{c}}
  {}&{{t_3} + {t_1}}&1
\end{array} \\
  \right|} \right|\]
Now solving with respect to Row 1 we get,
\[ \Rightarrow \] \[\Delta ' = \left| {\dfrac{1}{2}[({t_1} - {t_3}){t_2}.({t_2} - {t_1}) - ({t_2} - {t_1}){t_3}.({t_1} - {t_3})]} \right|\]
On simplification we get,

\[ \Rightarrow \] \[\Delta ' = \left| {\dfrac{1}{2}[{t_3}{t_1}{t_2} - {t_1}{t^2}_3 - {t_3}{t_2}^2 + {t_2}{t^2}_3 - {t^2}_1{t_2} + {t^2}_1{t_3} + {t_1}{t_2}^2 - {t_1}{t_2}{t_3})]} \right|\]
On taking \[{t_3}\] common from first 4 terms and on taking \[{t_1}\] common from last 4 terms we get,
\[ \Rightarrow \] \[\Delta ' = \left| {\dfrac{1}{2}[{t_3}({t_1}{t_2} - {t_1}{t_3} - {t_2}^2 + {t_2}{t_3}) - {t_1}({t_1}{t_2} - {t_1}{t_3} - {t_2}^2 + {t_2}{t_3})]} \right|\]
On taking terms common we get,
 \[ \Rightarrow \Delta ' = \left| {\dfrac{1}{2}[({t_3} - {t_1})({t_1}{t_2} - {t_1}{t_3} - {t_2}^2 + {t_2}{t_3})]} \right|\]
On taking \[{t_1}\] common from first two terms in the bracket, and on taking \[{t_2}\] common from last two terms in the bracket we get,
 \[ \Rightarrow \Delta ' = \left| {\dfrac{1}{2}[({t_3} - {t_1})({t_1}({t_2} - {t_3}) - {t_2}({t_2} - {t_3})]} \right|\]
On taking terms common we get,
\[ \Rightarrow \] \[\Delta ' = \left| {\dfrac{1}{2}({t_1} - {t_2})({t_2} - {t_3})({t_3} - {t_1})} \right|\]
As, \[\Delta = \left| {({t_1} - {t_2})({t_2} - {t_3})({t_3} - {t_1})} \right|\] , we get,
\[ \Rightarrow \] \[\Delta ' = \dfrac{1}{2}\Delta \]
On multiplying the equation by 2 we get,
\[ \Rightarrow \] \[\Delta = 2\Delta '\]
Hence, option (b) is the correct option.

Note: In this given problem we are trying to find the tangents of a parabola on a given point of the parabola. \[ky = 2ax + 2ah\] ,This is equation of a tangent to a parabola at a point \[(h,k).\]