
The tangent to the parabola
(a) (– 6, – 9)
(b) (– 13, – 9)
(c) (– 6, – 7)
(d) (13, 7)
Answer
504.9k+ views
Hint:In this question, firstly, find the equation of the tangent by differentiating the equation of parabola with respect to
Complete step by step answer:
We know, the point slope form of the equation,
To find the slope of the equation, we will differentiate the equation of the parabola with respect to
We know that,
Now, let us use the point-slope form of the equation which has
For the next step, we have the equation of the circle,
The standard form of the circle is
Therefore, the center of the given circle,
Let us draw the diagram from the obtained data and the given data for the parabola, circle and the tangent.
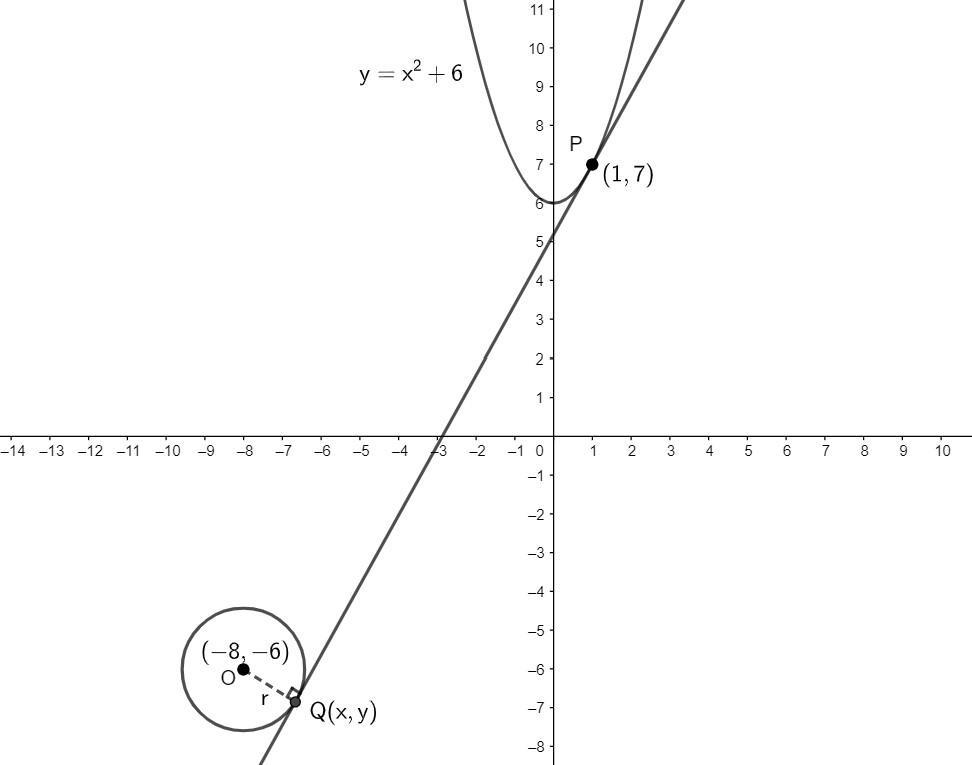
If we look closer to the circle and the tangent,
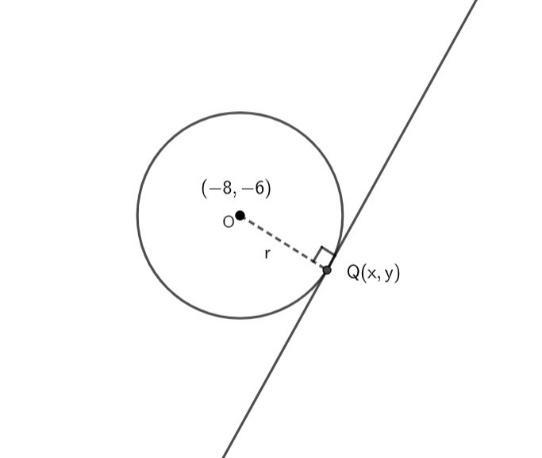
where,
Now, we know the distance between the two points, Q and O. So, let us use the distance formula between two points, and with the help of the trial and error method check which of the options is correct.
We know,
(a) (– 6, – 9):
(c) (– 6, – 7):
Note:
Here, there is another way to solve this question, simply use the trial and error method by substituting each option in the equation of tangent and if the total value equals to 0, then that relative point taken to get the value 0 is the correct answer.
Complete step by step answer:
We know, the point slope form of the equation,
To find the slope of the equation, we will differentiate the equation of the parabola with respect to
We know that,
Now, let us use the point-slope form of the equation which has
For the next step, we have the equation of the circle,
The standard form of the circle is
Therefore, the center of the given circle,
Let us draw the diagram from the obtained data and the given data for the parabola, circle and the tangent.

If we look closer to the circle and the tangent,

where,
Now, we know the distance between the two points, Q and O. So, let us use the distance formula between two points, and with the help of the trial and error method check which of the options is correct.
We know,
(a) (– 6, – 9):
(c) (– 6, – 7):
Note:
Here, there is another way to solve this question, simply use the trial and error method by substituting each option in the equation of tangent and if the total value equals to 0, then that relative point taken to get the value 0 is the correct answer.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 10 biology CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Why is there a time difference of about 5 hours between class 10 social science CBSE

Fill the blanks with proper collective nouns 1 A of class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

Change the following sentences into negative and interrogative class 10 english CBSE




