
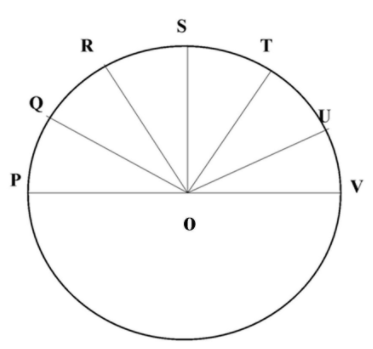
The table shows the number of three different brands of laptops sold by a certain store. The data are represented by the pie chart which shows a semicircle divided into six equal sectors. The angle representing the number of the Bell laptop is;
Brand Number of laptops Ace 60 Bell 40 Compact 20
(a)\[\angle POR\]
(b)\[\angle ROV\]
(c)\[\angle QOT\]
(d)\[\angle POU\]
| Brand | Number of laptops |
| Ace | 60 |
| Bell | 40 |
| Compact | 20 |

Answer
575.4k+ views
Hint: We must use a unitary method approach to solve this question. At first, we have to consider the whole circle to the total number of laptops. Then we have to estimate the angle of the sector defined by one laptop. We will find out the angle of the sector in the pie chart for the 40 laptops. In the next step we will find out the angles \[\angle PQR\], \[\angle ROV\], \[\angle QOT\] and \[\angle POU\]. Finally, we compare the obtained angle with the angle of the sector in the pie chart for the 40 laptops and find the correct one.
Complete step-by-step solution
The unitary method aims at determining values in relation to a single unit. In other words, we must find out the value of one unit and further use it to find the value of multiple units.
Now the total number of laptops is given by \[60+20+40=120\]
We know that the angle made by a complete rotation along the circumference is \[{{360}^{\circ }}\]. Consider the whole circle to the total number of laptops.
Then 120 laptops subtend \[{{360}^{\circ }}\]of the pie chart.
The angle of the sector subtended by one laptop is \[\dfrac{{{360}^{\circ }}}{120}={{3}^{\circ }}\]
Hence for the 40 number of Bell laptop, the angle of the sector is given by \[40\times {{3}^{\circ }}={{120}^{\circ }}\]
In the question, it is given that the semicircle is divided into 6 equal parts. We know that the angle subtended by a semicircle is\[{{180}^{\circ }}\]. Then the angle of each part is \[\dfrac{{{180}^{\circ }}}{6}={{30}^{\circ }}\] that means \[\angle POQ=\angle QOR=\angle ROS=\angle SOT=\angle TOU=\angle UOV={{30}^{\circ }}\].
Then,
\[\begin{align}
& \angle POR=\angle POQ+\angle QOR={{30}^{\circ }}+{{30}^{\circ }}={{60}^{\circ }} \\
& \angle ROV=\angle ROS+\angle SOT+\angle TOU+\angle UOV \\
& ={{30}^{\circ }}+{{30}^{\circ }}+{{30}^{\circ }}+{{30}^{\circ }} \\
& ={{120}^{\circ }} \\
& \angle QOT=\angle QOR+\angle ROS+\angle SOT \\
& ={{30}^{\circ }}+{{30}^{\circ }}+{{30}^{\circ }} \\
& ={{90}^{\circ }} \\
& \angle POU=\angle POQ+\angle QOR+\angle ROS+\angle SOT+\angle TOU \\
& ={{30}^{\circ }}+{{30}^{\circ }}+{{30}^{\circ }}+{{30}^{\circ }}+{{30}^{\circ }} \\
& ={{150}^{\circ }}
\end{align}\]
Therefore option (B) is correct.
Note: The angle subtended by a complete rotation along the circumference of a circle is \[{{360}^{\circ }}\]and along the circumference of a semicircle, the angle subtended is\[{{180}^{\circ }}\]. The semicircle is divided into 6 equal parts thus they have equal angles subtended at the center.
Complete step-by-step solution
The unitary method aims at determining values in relation to a single unit. In other words, we must find out the value of one unit and further use it to find the value of multiple units.
Now the total number of laptops is given by \[60+20+40=120\]
We know that the angle made by a complete rotation along the circumference is \[{{360}^{\circ }}\]. Consider the whole circle to the total number of laptops.
Then 120 laptops subtend \[{{360}^{\circ }}\]of the pie chart.
The angle of the sector subtended by one laptop is \[\dfrac{{{360}^{\circ }}}{120}={{3}^{\circ }}\]
Hence for the 40 number of Bell laptop, the angle of the sector is given by \[40\times {{3}^{\circ }}={{120}^{\circ }}\]
In the question, it is given that the semicircle is divided into 6 equal parts. We know that the angle subtended by a semicircle is\[{{180}^{\circ }}\]. Then the angle of each part is \[\dfrac{{{180}^{\circ }}}{6}={{30}^{\circ }}\] that means \[\angle POQ=\angle QOR=\angle ROS=\angle SOT=\angle TOU=\angle UOV={{30}^{\circ }}\].
Then,
\[\begin{align}
& \angle POR=\angle POQ+\angle QOR={{30}^{\circ }}+{{30}^{\circ }}={{60}^{\circ }} \\
& \angle ROV=\angle ROS+\angle SOT+\angle TOU+\angle UOV \\
& ={{30}^{\circ }}+{{30}^{\circ }}+{{30}^{\circ }}+{{30}^{\circ }} \\
& ={{120}^{\circ }} \\
& \angle QOT=\angle QOR+\angle ROS+\angle SOT \\
& ={{30}^{\circ }}+{{30}^{\circ }}+{{30}^{\circ }} \\
& ={{90}^{\circ }} \\
& \angle POU=\angle POQ+\angle QOR+\angle ROS+\angle SOT+\angle TOU \\
& ={{30}^{\circ }}+{{30}^{\circ }}+{{30}^{\circ }}+{{30}^{\circ }}+{{30}^{\circ }} \\
& ={{150}^{\circ }}
\end{align}\]
Therefore option (B) is correct.
Note: The angle subtended by a complete rotation along the circumference of a circle is \[{{360}^{\circ }}\]and along the circumference of a semicircle, the angle subtended is\[{{180}^{\circ }}\]. The semicircle is divided into 6 equal parts thus they have equal angles subtended at the center.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




