Question

The surface area of a sphere is the same as the curved surface area of a right circular cylinder whose height and diameter are 12 cm each. The radius of the sphere is:
(a) 3 cm
(b) 4 cm
(c) 6 cm
(d) 12 cm

Answer 1

Hint: First of all equate the surface area of a sphere with the curved surface area of a cylinder. The formula for the surface area of the sphere is $4\pi {{r}^{2}}$ and the curved surface area of the cylinder is 2πrh. Here r is the radius in both the solids and h is the depth of the cylinder. Then solving the equation will give us the radius of the sphere.

Complete step-by-step answer:
The formula for surface area of the sphere is $4\pi {{r}^{2}}$.
The below figure is of a sphere centred at A.

 The curved surface area of the cylinder is 2πrh.
The below figure is of a cylinder having radius 6cm and the height of the cylinder is 12cm.

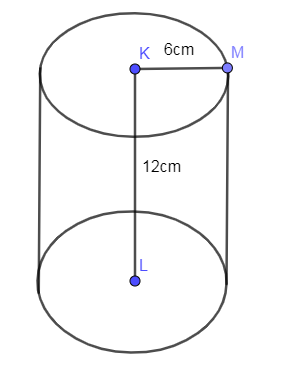
It is given that the height of the cylinder is 12 cm and the diameter of the cylinder is 12 cm. From the diameter of the cylinder, we can find the radius by dividing the diameter with 2 so the radius of the cylinder is 6 cm.
It is also given that surface area of sphere is equal to the curved surface area (C.S.A) of the cylinder so we are equating them and showing them as below:
Surface area of sphere = C. S. A of cylinder
$4\pi {{R}^{2}}=2\pi rh$
In the above equation R is the radius of the sphere, r is the radius of the cylinder and h is the depth of the cylinder. Now, substituting the values of r and h in the above equation, we get:
$\Rightarrow 4\pi {{R}^{2}}=2\pi \left( 6 \right)\left( 12 \right)$
In the above equation, π will be cancelled from both the sides and we get,
$\begin{align}
  & \Rightarrow 4{{R}^{2}}=2\left( 6 \right)\left( 12 \right) \\
 & \Rightarrow {{R}^{2}}=36 \\
\end{align}$
Taking square root on both the sides we get,
R= 6
So, the radius of the sphere is 6 cm.
Hence, the correct option is (c).

Note: After taking square root in the above solution,
$\begin{align}
  & {{R}^{2}}=36 \\
 & \Rightarrow R=\pm 6 \\
\end{align}$
You must be wondering ± should come. Yes, there will come 2 solutions: +6 or -6 but radius cannot be negative so we are taking only the positive solution of R.
And don’t forget to write the units of radius.