Question

The surface area of a cube is $ 1536c{m^2} $ .
Find:
(i) The length of its edge.
(ii) Its volume
(iii) The volume of its material whose thickness is $ 5mm. $

Answer 1

Hint: Use the formulae of surface area and volume of a cube. Also remember that the sides of a cube are equal. Using the following properties find the given parameters asked.

Complete step-by-step answer:

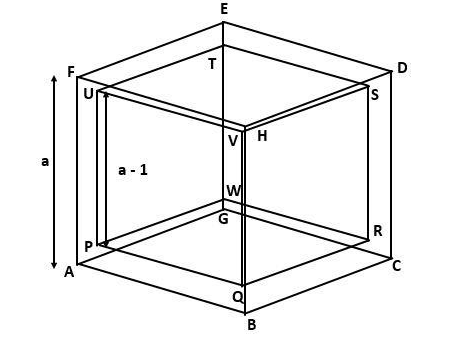
Let $ a $ be the side of the cube.
 $ S $ be the surface area of the cube.
 $ V $ be the volume of the cube.
 $ {V_m} $ be the volume of the material.

(i) We know that, surface area of a cube is the sum of the area of all the surfaces of the cube.
And every surface of a cube is square
 $ \therefore S = 6{a^2} $
It is given that,
 $ S = 1536c{m^2} $
 $ \therefore 6{a^2} = 1536c{m^2} $
Dividing both the sides by $ 6 $ , we get
 $ {a^2} = 256 $
Taking square root to both the sides, we get
 $ a = +16 $
Area cannot be $ - ve. $
 $ \therefore a = 16cm $
 $ \therefore $ length of its edge is $ 16cm. $

(ii) Now, volume of the cube is given by
 $ V = {a^3} $
 $ \Rightarrow V = {16^3} $ $ (\because a = 16) $
 $ \Rightarrow V = 4096c{m^3} $
Therefore, the volume of the cube is $ 4096c{m^3}. $

(iii) There is a material of thickness $ 5mm $ in the cube.
Let $ V' $ be the volume of the cube without material.
Then side of $ V' $ will be $ (a - 10mm) $ i.e. $ (a - 1)cm $
To get the length of the inner cube, we need to subtract $ 2 $ times the thickness from the original length. As the thickness of $ 5mm $ is to both the sides of the edge of the cube.
Therefore, volume of the cube inside the material is
 $ V' = {(a - 1)^3} $
 $ V' = {15^3} $ $ (\because a = 16) $
 $ V' = 3375c{m^3} $
Therefore, the volume of the material will be $ {V_m} = V - V' $
 $ \Rightarrow {V_m} = 4096 - 3375 $
 $ \Rightarrow {V_m} = 721c{m^3} $
Therefore, the volume of the material is $ 721c{m^3} $

Note: Sub question (iii) is tricky. You should understand that the material is not added to the given cube. But the cube is made by the material off thickness of $ 5mm. $ That means we need to subtract $ 1cm $ from the side of the cube. Do not add it.