
The sum of two point charges is\[7\mu C\]. They repel each other with a force of 1N when kept 30cm apart in free space. Calculate the value of each charge.
\[\begin{align}
& \text{A}\text{. 2}\mu C\text{ and 4}\mu C \\
& \text{B}\text{. 2}\mu C\text{ and 5}\mu C \\
& \text{C}\text{. 9}\mu C\text{ and 5}\mu C \\
& \text{D}\text{. 4}\mu C\text{ and 7}\mu C \\
\end{align}\]
Answer
585.6k+ views
Hint: According to the question, two charges are separated by a distance 30cm and they repel each other by force 1N. Hence we can conclude that there is Coulomb’s force and by using Coulomb’s law we can find the value of the charges. The sum of the two charges is also given by which we can find the exact values.
Formula used:
\[F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{1}}{{q}_{2}}}{{{r}^{2}}}\]
Complete answer:
According to Coulomb’s law, if two point charges \[{{q}_{1}}\text{ and }{{q}_{2}}\] are separated by a distance r then the F will be given as
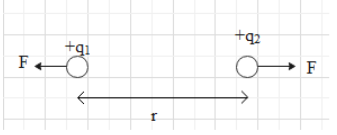
\[F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{1}}{{q}_{2}}}{{{r}^{2}}}\]
Here \[{{\varepsilon }_{0}}\]is the permittivity in free space and its value is \[8.85\times {{10}^{-12}}F{{m}^{-1}}\].
If both point charges have the same charge (i.e. negative or positive) they will repel and in case opposite charges are placed then they will attract.
According to the question, two point charges whose sum is \[7\mu C\] are placed at distance 30cm and they have a repulsive force of 1N in between them. Let us suppose the point charges are \[{{q}_{1}}\text{ and }{{q}_{2}}\]and from the given data\[F=1N,r=30cm=0.3m\text{ and }{{\varepsilon }_{0}}=8.85\times {{10}^{-12}}F{{m}^{-1}}\]. Then from the Coulomb’s law we can write,
\[\begin{align}
& 1=\dfrac{1}{4\pi \left( 8.85\times {{10}^{-12}} \right)}\dfrac{{{q}_{1}}{{q}_{2}}}{{{\left( 0.3 \right)}^{2}}} \\
& \Rightarrow {{q}_{1}}{{q}_{2}}=4\pi \left( 8.85\times {{10}^{-12}} \right){{\left( 0.3 \right)}^{2}} \\
& \Rightarrow {{q}_{1}}{{q}_{2}}=4\times 3.14\times 8.85\times 0.09\times {{10}^{-12}} \\
& \Rightarrow {{q}_{1}}{{q}_{2}}\simeq 10\times {{10}^{-12}}C\text{ }..............\text{(i)} \\
\end{align}\]
Now we have given the sum of \[{{q}_{1}}\text{ and }{{q}_{2}}\], so we can write
\[\begin{align}
& \Rightarrow {{q}_{1}}+{{q}_{2}}=7\mu C \\
& \Rightarrow {{q}_{1}}+{{q}_{2}}=7\times {{10}^{-6}}C \\
& \Rightarrow {{q}_{1}}=7\times {{10}^{-6}}-{{q}_{2}}\text{ }.................\text{(ii)} \\
\end{align}\]
Substituting value of \[{{q}_{1}}\]from (ii), in equation (i)
\[\begin{align}
& \Rightarrow \left( 7\times {{10}^{-6}}-{{q}_{2}} \right){{q}_{2}}=10\times {{10}^{-12}} \\
& \Rightarrow 7\times {{10}^{-6}}{{q}_{2}}-q_{2}^{2}=10\times {{10}^{-12}} \\
& \Rightarrow q_{2}^{2}-7\times {{10}^{-6}}{{q}_{2}}+10\times {{10}^{-12}}=0 \\
& \Rightarrow q_{2}^{2}+(5+2)\times {{10}^{-6}}{{q}_{2}}+10\times {{10}^{-12}}=0 \\
& \Rightarrow q_{2}^{2}+5\times {{10}^{-6}}{{q}_{2}}-2\times {{10}^{-6}}{{q}_{2}}+10\times {{10}^{-12}}=0 \\
& \Rightarrow {{q}_{2}}({{q}_{2}}+5\times {{10}^{-6}})-2\times {{10}^{-6}}({{q}_{2}}+5\times {{10}^{-6}})=0 \\
& \Rightarrow ({{q}_{2}}-2\times {{10}^{-6}})({{q}_{2}}+5\times {{10}^{-6}})=0 \\
& \Rightarrow {{q}_{2}}=2\times {{10}^{-6}}C\text{ or }{{q}_{2}}=-5\times {{10}^{-6}}C \\
& \Rightarrow {{q}_{2}}=2\mu C\text{ or }{{q}_{2}}=-5\mu C \\
\end{align}\]
Substituting values of \[{{q}_{2}}\]in equation (ii) we get the values of \[{{q}_{1}}\]which are given below
\[{{q}_{1}}=5\mu C\text{ or }{{q}_{1}}=9\mu C\]
As the point charges repel therefore they will have the same charges (here positive). Hence the point charges have values\[{{q}_{1}}=5\mu C\text{ or }{{q}_{2}}=2\mu C\].
Hence option B is correct.
Note:
We can directly conclude that the right answer is B as the sum of charges should be \[7\mu C\] and the only option whose sum is \[7\mu C\], is option B. Although option C can be correct if attractive force was considered but it is given that force is repulsive force. In case there is attractive force then there will be opposite charges and the direction of force experienced by point charges will be towards each other.
Formula used:
\[F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{1}}{{q}_{2}}}{{{r}^{2}}}\]
Complete answer:
According to Coulomb’s law, if two point charges \[{{q}_{1}}\text{ and }{{q}_{2}}\] are separated by a distance r then the F will be given as
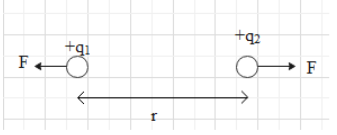
\[F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{1}}{{q}_{2}}}{{{r}^{2}}}\]
Here \[{{\varepsilon }_{0}}\]is the permittivity in free space and its value is \[8.85\times {{10}^{-12}}F{{m}^{-1}}\].
If both point charges have the same charge (i.e. negative or positive) they will repel and in case opposite charges are placed then they will attract.
According to the question, two point charges whose sum is \[7\mu C\] are placed at distance 30cm and they have a repulsive force of 1N in between them. Let us suppose the point charges are \[{{q}_{1}}\text{ and }{{q}_{2}}\]and from the given data\[F=1N,r=30cm=0.3m\text{ and }{{\varepsilon }_{0}}=8.85\times {{10}^{-12}}F{{m}^{-1}}\]. Then from the Coulomb’s law we can write,
\[\begin{align}
& 1=\dfrac{1}{4\pi \left( 8.85\times {{10}^{-12}} \right)}\dfrac{{{q}_{1}}{{q}_{2}}}{{{\left( 0.3 \right)}^{2}}} \\
& \Rightarrow {{q}_{1}}{{q}_{2}}=4\pi \left( 8.85\times {{10}^{-12}} \right){{\left( 0.3 \right)}^{2}} \\
& \Rightarrow {{q}_{1}}{{q}_{2}}=4\times 3.14\times 8.85\times 0.09\times {{10}^{-12}} \\
& \Rightarrow {{q}_{1}}{{q}_{2}}\simeq 10\times {{10}^{-12}}C\text{ }..............\text{(i)} \\
\end{align}\]
Now we have given the sum of \[{{q}_{1}}\text{ and }{{q}_{2}}\], so we can write
\[\begin{align}
& \Rightarrow {{q}_{1}}+{{q}_{2}}=7\mu C \\
& \Rightarrow {{q}_{1}}+{{q}_{2}}=7\times {{10}^{-6}}C \\
& \Rightarrow {{q}_{1}}=7\times {{10}^{-6}}-{{q}_{2}}\text{ }.................\text{(ii)} \\
\end{align}\]
Substituting value of \[{{q}_{1}}\]from (ii), in equation (i)
\[\begin{align}
& \Rightarrow \left( 7\times {{10}^{-6}}-{{q}_{2}} \right){{q}_{2}}=10\times {{10}^{-12}} \\
& \Rightarrow 7\times {{10}^{-6}}{{q}_{2}}-q_{2}^{2}=10\times {{10}^{-12}} \\
& \Rightarrow q_{2}^{2}-7\times {{10}^{-6}}{{q}_{2}}+10\times {{10}^{-12}}=0 \\
& \Rightarrow q_{2}^{2}+(5+2)\times {{10}^{-6}}{{q}_{2}}+10\times {{10}^{-12}}=0 \\
& \Rightarrow q_{2}^{2}+5\times {{10}^{-6}}{{q}_{2}}-2\times {{10}^{-6}}{{q}_{2}}+10\times {{10}^{-12}}=0 \\
& \Rightarrow {{q}_{2}}({{q}_{2}}+5\times {{10}^{-6}})-2\times {{10}^{-6}}({{q}_{2}}+5\times {{10}^{-6}})=0 \\
& \Rightarrow ({{q}_{2}}-2\times {{10}^{-6}})({{q}_{2}}+5\times {{10}^{-6}})=0 \\
& \Rightarrow {{q}_{2}}=2\times {{10}^{-6}}C\text{ or }{{q}_{2}}=-5\times {{10}^{-6}}C \\
& \Rightarrow {{q}_{2}}=2\mu C\text{ or }{{q}_{2}}=-5\mu C \\
\end{align}\]
Substituting values of \[{{q}_{2}}\]in equation (ii) we get the values of \[{{q}_{1}}\]which are given below
\[{{q}_{1}}=5\mu C\text{ or }{{q}_{1}}=9\mu C\]
As the point charges repel therefore they will have the same charges (here positive). Hence the point charges have values\[{{q}_{1}}=5\mu C\text{ or }{{q}_{2}}=2\mu C\].
Hence option B is correct.
Note:
We can directly conclude that the right answer is B as the sum of charges should be \[7\mu C\] and the only option whose sum is \[7\mu C\], is option B. Although option C can be correct if attractive force was considered but it is given that force is repulsive force. In case there is attractive force then there will be opposite charges and the direction of force experienced by point charges will be towards each other.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




