Question

The sum of the measures of the interior angles of a polygon of n sides is equal to which of the following
(a) 2n right angles
(b) (2n – 2) right angles
(c) 2 (n – 2) right angles
(d) 4 (n – 2) right angles.

Answer 1

Hint: Draw a polygon of n sides. Choose a vertex and draw diagonals from it. You will get (n – 2) triangles. Use the fact that the sum of interior angles of a triangle is $180{}^\circ $. Find the sum of all these triangles to get the final answer.

Complete step-by-step solution:
In this question, we need to find the sum of the measures of the interior angles of a polygon of n sides.
We will do this by the following method:
Step 1: Draw a polygon of n sides.
Step 2: Choose any one vertex from the n vertices.
Step 3: Name that vertex as A1 and then start naming the other vertices in order: A2, A3, and so on.
Step 4: Draw a line and join all the vertices to A1.
Following these steps, we will get the following figure:

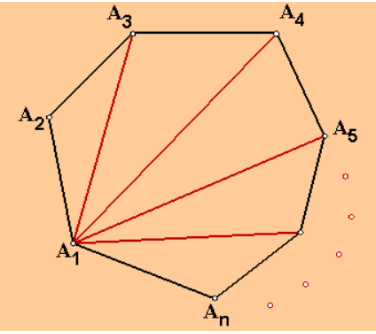
As we can see from the above diagram, we have drawn (n – 3) diagonals from the point A1.
These diagonals divide the n sided polygon into (n – 2) triangles with all the interior angles of the triangles lying on the interior angles of the n sided polygon.
So, there are (n – 2) triangles altogether.
We know that the sum of interior angles of a triangle is $180{}^\circ $.
We have (n – 2) triangles.
So, the sum of all the interior angles of the polygon = sum of the interior angles of all the triangles = $\left( n-2 \right)\times 180{}^\circ $
Now, we know that $180{}^\circ $ = 2 right angles
So, the sum of all the interior angles of the polygon = 2 (n – 2) right angles
Hence, option (c) is correct.

Note: We can also solve this question by another approach. Instead of drawing diagonals from one of the vertices, we can choose any interior point of the polygon and join it to the vertices to form n triangles. Find the sum of the angles of all these triangles and then subtract $360{}^\circ $ from it as the interior point chosen is not on any vertex and hence, does not contribute to the sum of all the interior angles of the polygon.