Question

The sum of lengths of the hypotenuse and a side of a right angled triangle is given. Show that the area of the triangle is maximum when the angle between them is $60^\circ $?

Answer 1

Hint: Here we will construct a diagram on the basis of given parameters. After that we will find the area of the right angle triangle. Then we will differentiate it with respect to x and find values of maximum value of it. Calculate value of required angle at this value.

Complete step-by-step answer:

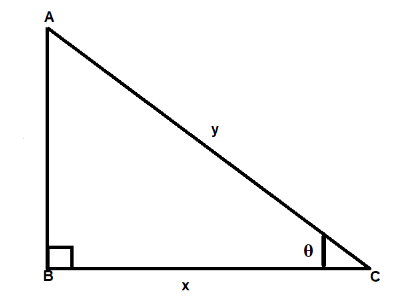
According to the question $\Delta ABC$ is an right angle triangle, in which $BC = x,AC = y$
Now we find the value of the side AB by Pythagoras theorem, we get
\[AC^2 = AB^2 + BC^2\]
Now putting the value of BC and AC we get
${x^2} = {y^2} + A{B^2}$
By solving this we get,
$
  A{B^2} = {x^2} - {y^2} \\
  AB = \sqrt {{x^2} - {y^2}} \\
 $
Now apply formula of area of right angle triangle
$Area = \dfrac{1}{2} \times BC \times AB$
Now we put the values in the above formula we get,
Area = $\dfrac{1}{2}x\sqrt {{y^2} - {x^2}} $
Now we square both sides we get,
\[Are{a^2} = \dfrac{{{x^2}({y^2} - {x^2})}}{4}\]
Now we put \[y = \left( {k - x} \right)\], $\because x + y = k(cons\tan t)$ we get
$Are{a^2} = \dfrac{{{x^{^2}}\left[ {{{\left( {k - x} \right)}^2} - {x^2}} \right]}}{4}$
Now we solve the above equation we apply the formula as ${(a - b)^2} = {a^2} + {b^2} - 2ab$ we get
$Are{a^2} = \dfrac{{{x^{^2}}\left[ {{k^2} + {x^2} - 2kx - {x^2}} \right]}}{4}$
Now simplifying the equation we get
$Are{a^2} = \dfrac{{{x^{^2}}\left[ {{k^2} - 2kx} \right]}}{4}$
Now multiply the numerator by ${x^2}$ we get
 $Are{a^2} = \dfrac{{{k^2}{x^2} - 2k{x^3}}}{4}$ $ \cdot \cdot \cdot \left( i \right)$
Now On differentiating$\left( i \right)$, We get
$2Area.\dfrac{{dA}}{{dx}} = \dfrac{{2{k^2}x - 6k{x^2}}}{4}$ $ \cdot \cdot \cdot \left( {ii} \right)$
After simplifying the above equation we get
$\dfrac{{dA}}{{dx}} = \dfrac{{{k^2}x - 3k{x^2}}}{{4A}}$
Now, as we know that
$
   \Rightarrow \dfrac{{dA}}{{dx}} = 0 \\
  we{\text{ }}put{\text{ }}the{\text{ }}value{\text{ }}of\dfrac{{dA}}{{dx}}, \\
   \Rightarrow \left( {{k^2}x - 3k{x^2}} \right) = 0 \\
  after{\text{ }}simplifying{\text{ }}we{\text{ }}get \\
   \Rightarrow x = \dfrac{k}{3} \\
 $
Here we are neglecting $x = 0$
Thus, A is maximum when $x = \dfrac{k}{3}$
Now, we put the value of x in the equation \[y = \left( {k - x} \right)\] we get
 $
   \Rightarrow y = \left( {k - \dfrac{k}{3}} \right) \\
  y = \left( {\dfrac{{2k}}{3}} \right) \\
 $
Now $\cos \theta = \dfrac{{BC}}{{AC}}$, putting the value we get
$\therefore \dfrac{x}{y} = \cos \theta $
Now we put the value of x, y we get
$
   \Rightarrow \cos \theta = \dfrac{{\left( {\dfrac{k}{3}} \right)}}{{\left( {\dfrac{{2k}}{3}} \right)}} \\
   \Rightarrow \cos \theta = \dfrac{1}{2} \\
 $
Hence the value of
$ \Rightarrow \theta = \dfrac{\pi }{3}$

Hence, the area is maximum when $\theta = 60^\circ $

Note: Here we can apply differentiation for finding the value of maxima, because we know that maximum is obtained when differentiation will be negative .So for that we have to find differentiation to make it equal zero and get maximum value.