Question

The sum of both the curved surfaces of the hollow metallic cylinder is $1408c{m^2}$ and the volume of the metal in it is $1408c{m^3}$. Find the thickness of the metal in this cylinder if its height is 28 cm.

Answer 1

Hint: As we are asked to find the thickness of the hollow metallic cylinder it is just the difference between the outer radius and inner radius and using the formula $CSA = 2\pi rh$ and given that the sum of the curved surface areas is $1408c{m^2}$we get the value of R + r . And using the known values in the volume formula we get the value of R – r .

Complete step-by-step answer:
We are given a hollow metallic cylinder
Let the inner radius be r cm and the outer radius be R cm

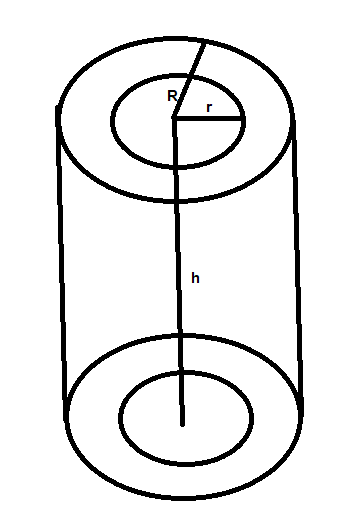
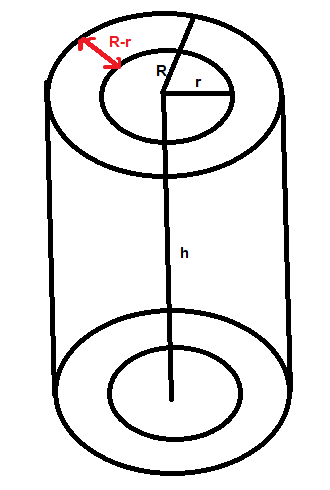
We need to find the thickness and it is nothing but the difference between the outer radius and inner radius
$ \Rightarrow thickness = R - r$

We know that the curved surface of the cylinder is given by the formula
$ \Rightarrow CSA = 2\pi rh$
Where r is the radius and h is the height of the cylinder
Here we are given that the sum of the curved surface areas is $1408c{m^2}$
That is
$ \Rightarrow 2\pi rh + 2\pi Rh = 1408c{m^2}$
As we are given the height of the cylinder to be 28 cm
\[
   \Rightarrow 2\pi h\left( {r + R} \right) = 1408c{m^2} \\
   \Rightarrow \pi \left( {r + R} \right) = \dfrac{{1408c{m^2}}}{{2*28}} \\
   \Rightarrow \left( {r + R} \right) = \dfrac{{704}}{{28}}*\dfrac{7}{{22}} = \dfrac{{64}}{8} \\
   \Rightarrow \left( {r + R} \right) = 8cm \\
 \]
Let this be equation (1)
We are given the volume of the metal in it to be $1408c{m^3}$
Volume of a hollow cylinder is given by
$ \Rightarrow Volume = \pi h\left( {{R^2} - {r^2}} \right)$
This can also be written as
$ \Rightarrow Volume = \pi h\left( {R + r} \right)\left( {R - r} \right)$
Substituting the known values in the formula we get
$
   \Rightarrow 1408 = \dfrac{{22}}{7}*28*8*\left( {R - r} \right) \\
   \Rightarrow \dfrac{{1408*7}}{{22*28*8}} = \left( {R - r} \right) \\
   \Rightarrow \dfrac{{128*1}}{{2*4*8}} = \left( {R - r} \right) \\
   \Rightarrow \dfrac{{128}}{{64}} = \left( {R - r} \right) \\
   \Rightarrow \left( {R - r} \right) = 2cm \\
$
2cm is the required thickness of the hollow metallic cylinder.
Note: A hollow cylinder is made up of two thin sheets of rectangle having a length and breadth
A hollow cylinder is one which is empty from inside and has some difference between the internal and external radius.
In a hollow cylinder, there are two curved surface areas: inner and outer and one circular base with inner and outer surface area.