Question

The students of a Vidyalaya were asked to participate in a competition for making and decorating penholders in the shape of a cylinder with a base, using cardboard. Each penholder was to be of radius 3 cm and height 10.5 cm. The Vidyalaya was to supply the competitors with cardboard. If there were 35 competitors, how much cardboard was required to be bought for the competition?

Answer 1

Hint: As given in the question, pen holders must be made in the shape of a cylinder. One side of the cylinder must be opened and one side must be closed to hold the pens i.e. open at the top and closed at the bottom. So, along with the curved surface area of the cylinder we have to calculate the area of the base. The base of the cylinder will be in a circle. For 35 competitors, the cardboard to be bought should make 35 penholders. So multiply the area of one pen holder with 35 to get the required cardboard area.
Formula used: Curved surface area of the cylinder is $2\pi rh$ where ‘r’ is the radius of the base of the cylinder, ‘h’ is the height of the cylinder.
Area of the circle (base) is $\pi {r^2}$ where ‘r’ is the radius of the base.

Complete Step-by-step Solution

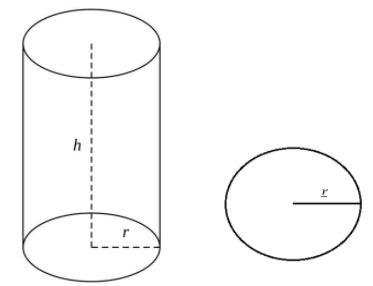
We are given that the height of the penholder is 10.5cm, base radius of the penholder is 3cm.
We have to calculate the curved surface area of the penholder and the area of the circle (bottom) to get the required cardboard area of a penholder.
Total area of the penholder= Curved surface area of the penholder + Area of the base circle of the penholder.
Which is \[2\pi rh + \pi {r^2}\]
$\pi = \dfrac{{22}}{7},r = 3cm,h = 10.5cm$
Now, substitute the above values in the total area formula.

Total area = $2\pi rh + \pi {r^2}$
\[
   = \left( {2 \times \dfrac{{22}}{7} \times 3 \times 10.5} \right) + \left( {\dfrac{{22}}{7} \times 3 \times 3} \right) \\
   = \dfrac{{22}}{7} \times 3\left( {\left( {2 \times 10.5} \right) + 3} \right) \\
   = \dfrac{{66}}{7}\left( {21 + 3} \right) \\
   = \dfrac{{66 \times 24}}{7} \\
   = \dfrac{{1584}}{7}c{m^2} \\
 \]
So, to make one penholder by a competitor we require $\dfrac{{1584}}{7}c{m^2}$ of cardboard to be bought.
For 35 competitors, we require $35 \times \dfrac{{1584}}{7}c{m^2}$ of cardboard to make 35 penholders.
$
   \to 35 \times \dfrac{{1584}}{7} \\
   \to 3{{{5}}^5} \times \dfrac{{1584}}{{{{{7}}_1}}} \\
   \to 5 \times 1584 \\
   \to 7920c{m^2} \\
 $
Therefore, $7920$ square centimeter of cardboard was required to be bought for the competition conducted by Vidyalaya for 35 competitors.

Note: Curved surface area of the cylinder excludes the bases. While calculating the total required cardboard area, do not add the area of the opened circle i.e. top circle. Another approach to solve this problem is to subtract the area of the top from the total surface area of the pen holder.