
The string of a kite is 50m long and it makes an angle of 60 degree with the horizontal. find the height of the kite above the ground
Answer
594.6k+ views
Hint: in this type of question we should be familiar with trigonometric concept
As we know \[\sin \theta = \dfrac{{perpendicular}}{{hypotenuse}}\]
\[\sin 60 = \dfrac{{\sqrt 3 }}{2}\]
String will be considered as hypotenuse
Given: the string of a kite is 50m long and it makes an angle of 60 degree with the horizontal
Complete step-by-step answer:
When we are solving this type of question, we need to follow the steps provided in the hint part above.
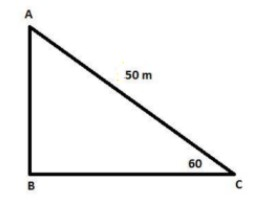
Since we have given that
Length of string (AB)of kite = 50 m
Angle of elevation formed by a kite with the horizontal = 60°
We need to find the height of the kite.
Consider Δ ABC, as shown in the figure:
\[\begin{array}{l}
\sin 60 = \dfrac{{AB}}{{AC}}\\
\dfrac{{\sqrt 3 }}{2} = \dfrac{{AB}}{{50}}\\
\dfrac{{50\sqrt 3 }}{2} = AB\\
AB = 25\sqrt 3 \,\,m
\end{array}\]
Hence, the height of the kite is \[25\sqrt 3 \]m.
Hence after following the each and every step given in the hint part we obtained our final answer.
Additional Information:Here we can clearly see that in this solution we did not use any complicated process because we followed basic and simple things in the right order as per given in the above hint section.
Note:
We need to use right formula to calculate the required value and the value calculated from this should also be accurate.
As we know \[\sin \theta = \dfrac{{perpendicular}}{{hypotenuse}}\]
\[\sin 60 = \dfrac{{\sqrt 3 }}{2}\]
String will be considered as hypotenuse
Given: the string of a kite is 50m long and it makes an angle of 60 degree with the horizontal
Complete step-by-step answer:
When we are solving this type of question, we need to follow the steps provided in the hint part above.

Since we have given that
Length of string (AB)of kite = 50 m
Angle of elevation formed by a kite with the horizontal = 60°
We need to find the height of the kite.
Consider Δ ABC, as shown in the figure:
\[\begin{array}{l}
\sin 60 = \dfrac{{AB}}{{AC}}\\
\dfrac{{\sqrt 3 }}{2} = \dfrac{{AB}}{{50}}\\
\dfrac{{50\sqrt 3 }}{2} = AB\\
AB = 25\sqrt 3 \,\,m
\end{array}\]
Hence, the height of the kite is \[25\sqrt 3 \]m.
Hence after following the each and every step given in the hint part we obtained our final answer.
Additional Information:Here we can clearly see that in this solution we did not use any complicated process because we followed basic and simple things in the right order as per given in the above hint section.
Note:
We need to use right formula to calculate the required value and the value calculated from this should also be accurate.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




