Question

The stream of water is flowing with a speed of$2km/h.$A swimmer can swim at a speed of$4km/h.$ What should be the direction of the swimmer with respect to the flow of the river to cross the river straight?
(A) ${60^ \circ }$
(B) ${150^ \circ }$
(C) ${90^ \circ }$
(D) ${120^ \circ }$

Answer 1

Hint
To solve this question, assume the direction of the swimmer and divide the velocity of the swimmer into two perpendicular components. Then apply the given condition to get the final answer.

Complete step by step answer
Let the swimmer swim at an angle of$\theta $with the flow of the river. Also, let ${V_r}$and ${V_s}$be the velocities of the river and the swimmer.

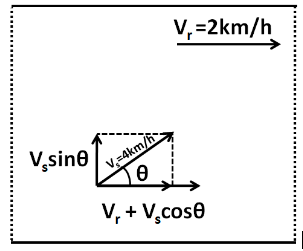
During swimming, the velocity of the river will get added to the component of the velocity of the swimmer along the flow of the river. To cross the river straight, the resultant velocity of the swimmer should be perpendicular to the direction of the flow of the river. That is, the horizontal component of the resultant velocity of the swimmer should be zero.
The division of the swimmer’s velocity into perpendicular components is shown in the figure above. As we can clearly see in the figure, the horizontal component of the resultant velocity is equal to ${V_r} + {V_s}\cos \theta $, which should be zero, i.e.
${V_r} + {V_s}\cos \theta = 0$
 According to the question, ${V_r} = 2km/h$ and${V_s} = 4km/h$. Substituting these in the above equation
$2 + 4\cos \theta = 0$
$4\cos \theta = - 2$
Dividing by $4$, we have
$\cos \theta = - \dfrac{1}{2}$
This finally gives
$\theta = {120^ \circ }$
So, for crossing the river straight, the swimmer has to swim at an angle of ${120^ \circ }$ with the flow of the river.
Hence, the correct answer is option D, ${120^ \circ }$.

Note
For solving such types of questions, always divide the resultant velocity of the swimmer into two perpendicular components, one along the flow of the river, and the other perpendicular to the flow. Then apply the required conditions on the two components. Do not try to attempt such questions physically, as the chances of committing the mistakes are high in these.