Question

The straight lines \[x+2y-9=0,\,\,3x=5y-5=0\,\text{and}\,ax+by+1=0\] are concurrent, if the straight line \[35x-22y+1=0\] passes through the point
A.\[(a,b)\]
B.\[(b,a)\]
C.\[(-a,-b)\]
D.None of these

Answer 1

Hint: In this particular problem, it has been mentioned that the three equations are concurrent, which means two non-parallel intersect at one point. If a third line formed passed through one common point or intersecting at one common point, these straight lines are termed as concurrent lines Another way we can say that determinant \[\Delta =0\]to find the points which are passing through the equation.

Complete step-by-step answer:
In this type of problems there are three equation is given that is
\[x+2y-9=0---(1)\]
\[3x+5y-5=0---(2)\]
\[ax+by+1=0---(3)\]

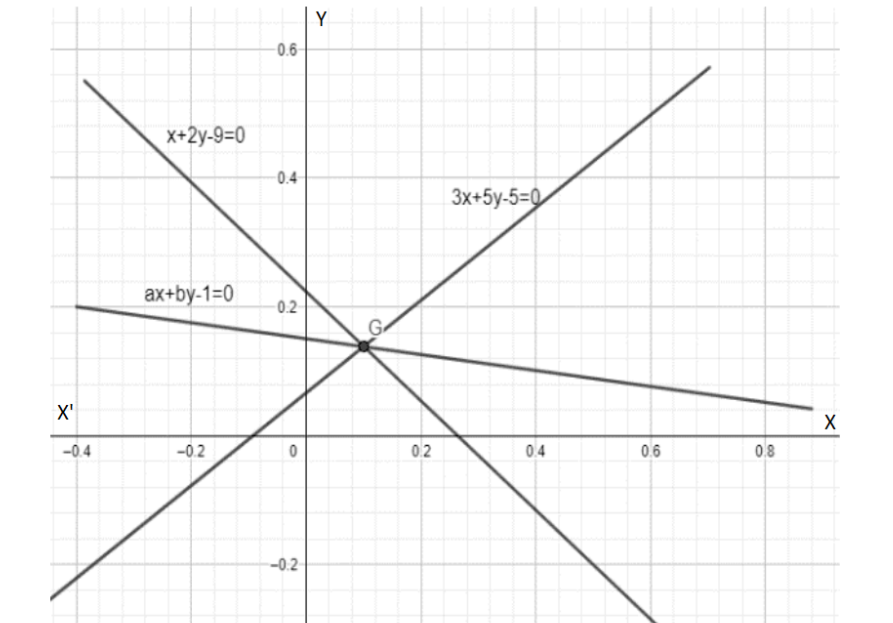
Above figures show that three lines of equation are intersecting at a common point that is called concurrent lines.
Another way we can also say that to satisfy the three equations concurrent determinants should be Zero.
It is represented as \[\Delta =\left| \begin{matrix}
   {{a}_{1}} & {{b}_{1}} & {{c}_{1}} \\
   {{a}_{2}} & {{b}_{2}} & {{c}_{2}} \\
   {{a}_{3}} & {{b}_{3}} & {{c}_{3}} \\
\end{matrix} \right|=0\]
So, first of all there are three equation so, this three equation can be written in the form of determinant
\[\Delta =\left| \begin{matrix}
   1 & 2 & -9 \\
   3 & 5 & -5 \\
   a & b & -1 \\
\end{matrix} \right|=0\]
By simplifying the above equation we get:
\[1(-5-(-5b))-2(-3-(-5a))+(-9)(3b-5a)=0\]
By simplifying and further solving we get:
\[1(-5+5b)-2(-3+5a)-9(3b-5a)=0\]
After expanding this above equation we get:
\[-5+5b+6-10a-27b+45a=0\]
After simplifying and further solving this above equation we get:
\[35a-22b+1=0--(1)\]
And another equation which we have is \[35x-22y+1=0--(2)\]
So comparing equation (1) and (2) we get:
We can say that the equation (2) is passed through a point that is \[(a,b)\]
So, the correct option is “option A”.
So, the correct answer is “Option A”.

Note: In this problem always remember the condition which is used in case of concurrent lines. Only we have to use the condition that the determinant should be 0. And simplifying the step and comparing with the original equation which is given you will get the points. Don’t get confused between concurrent lines and intersection lines. More than two lines that meet at common points are concurrent lines and only two points that intersect at common points are called intersection lines.