Question

The straight lines represented by \[{\left( {y - mx} \right)^2} = {a^2}\left( {1 + {m^2}} \right)\] and \[{\left( {y - nx} \right)^2} = {a^2}\left( {1 + {n^2}} \right)\] form a
(a) rectangle
(b) rhombus
(c) trapezium
(d) None of these

Answer 1

Hint: Here, we need to find the shape formed by the given straight lines equation. First, we will take the square root of the two equations and simplify it to find the equations of the four lines required to form a shape. These lines are linear equations in two variables. We will compare the ratios of the coefficients of two lines to get the pair of parallel lines. Then, we will use the distance formula between two parallel lines to find the two altitudes of the quadrilateral. Finally, we will use the formula for the area of a parallelogram to find the shape of the quadrilateral formed.

Formula Used:
We will use the following formulas:
1. The linear equations in two variables \[{a_1}x + {b_1}y + {c_1} = 0\] and \[{a_2}x + {b_2}y + {c_2} = 0\] have no solution if \[\dfrac{{{a_1}}}{{{a_2}}} = \dfrac{{{b_1}}}{{{b_2}}} \ne \dfrac{{{c_1}}}{{{c_2}}}\].
2. The distance between two parallel lines \[ax + by + {c_1} = 0\] and \[ax + by + {c_2} = 0\] is given by the formula \[d = \dfrac{{\left| {{c_2} - {c_1}} \right|}}{{\sqrt {{a^2} + {b^2}} }}\].

Complete step-by-step answer:
First, we will find the straight lines by simplifying the given equations.
Taking the square root of both sides of the equation \[{\left( {y - mx} \right)^2} = {a^2}\left( {1 + {m^2}} \right)\], we get
\[\begin{array}{l} \Rightarrow \sqrt {{{\left( {y - mx} \right)}^2}} = \sqrt {{a^2}\left( {1 + {m^2}} \right)} \\ \Rightarrow y - mx = \pm a\sqrt {1 + {m^2}} \end{array}\]
Thus, we get the equations
\[ \Rightarrow y - mx = a\sqrt {1 + {m^2}} \] and \[y - mx = - a\sqrt {1 + {m^2}} \]
Let the straight lines represented by the equations \[y - mx = a\sqrt {1 + {m^2}} \] and \[y - mx = - a\sqrt {1 + {m^2}} \] be \[p\] and \[q\] respectively.
Now, we will check the number of solutions of the lines \[p\] and \[q\].
We can observe that the lines \[y - mx = a\sqrt {1 + {m^2}} \] and \[y - mx = - a\sqrt {1 + {m^2}} \] are linear equations in two variables.
The linear equations in two variables \[{a_1}x + {b_1}y + {c_1} = 0\] and \[{a_2}x + {b_2}y + {c_2} = 0\] have unique solution if \[\dfrac{{{a_1}}}{{{a_2}}} \ne \dfrac{{{b_1}}}{{{b_2}}}\].
The linear equations in two variables \[{a_1}x + {b_1}y + {c_1} = 0\] and \[{a_2}x + {b_2}y + {c_2} = 0\] have infinitely many solutions if \[\dfrac{{{a_1}}}{{{a_2}}} = \dfrac{{{b_1}}}{{{b_2}}} = \dfrac{{{c_1}}}{{{c_2}}}\].
The linear equations in two variables \[{a_1}x + {b_1}y + {c_1} = 0\] and \[{a_2}x + {b_2}y + {c_2} = 0\] have no solution if \[\dfrac{{{a_1}}}{{{a_2}}} = \dfrac{{{b_1}}}{{{b_2}}} \ne \dfrac{{{c_1}}}{{{c_2}}}\].
Rewriting the equations of the lines, we get
\[ - mx + y - a\sqrt {1 + {m^2}} = 0\] and \[ - mx + y + a\sqrt {1 + {m^2}} = 0\]
Comparing \[ - mx + y - a\sqrt {1 + {m^2}} = 0\] to the standard form \[{a_1}x + {b_1}y + {c_1} = 0\], we get
\[{a_1} = - m\], \[{b_1} = 1\], and \[{c_1} = - a\sqrt {1 + {m^2}} \]
Comparing \[ - mx + y + a\sqrt {1 + {m^2}} = 0\] to the standard form \[{a_2}x + {b_2}y + {c_2} = 0\], we get
\[{a_2} = - m\], \[{b_2} = 1\], and \[{c_2} = a\sqrt {1 + {m^2}} \]
Now, we will find the ratios of the coefficients of \[x\], \[y\], and the constant.
Dividing \[{a_1} = - m\] by \[{a_2} = - m\], we get
\[\dfrac{{{a_1}}}{{{a_2}}} = \dfrac{{ - m}}{{ - m}} = 1\]
Dividing \[{b_1} = 1\] by \[{b_2} = 1\], we get
\[\dfrac{{{b_1}}}{{{b_2}}} = \dfrac{1}{1} = 1\]
Dividing \[{c_1} = - a\sqrt {1 + {m^2}} \] by \[{c_2} = a\sqrt {1 + {m^2}} \], we get
\[\dfrac{{{c_1}}}{{{c_2}}} = \dfrac{{ - a\sqrt {1 + {m^2}} }}{{a\sqrt {1 + {m^2}} }} = - 1\]
We can observe that \[\dfrac{{{a_1}}}{{{a_2}}} = \dfrac{{{b_1}}}{{{b_2}}} \ne \dfrac{{{c_1}}}{{{c_2}}}\].
Therefore, the lines \[ - mx + y - a\sqrt {1 + {m^2}} = 0\] and \[ - mx + y + a\sqrt {1 + {m^2}} = 0\] have no solution.
This means that the lines \[p\] and \[q\] are parallel lines.
Taking the square root on both sides \[{\left( {y - nx} \right)^2} = {a^2}\left( {1 + {n^2}} \right)\], we get
\[\begin{array}{l} \Rightarrow \sqrt {{{\left( {y - nx} \right)}^2}} = \sqrt {{a^2}\left( {1 + {n^2}} \right)} \\ \Rightarrow y - nx = \pm a\sqrt {1 + {n^2}} \end{array}\]
Thus, we get the equations
\[ \Rightarrow y - nx = a\sqrt {1 + {n^2}} \] and \[y - nx = - a\sqrt {1 + {n^2}} \]
Let the straight lines represented by the equations \[y - nx = a\sqrt {1 + {n^2}} \] and \[y - nx = - a\sqrt {1 + {n^2}} \] be \[r\] and \[s\] respectively.
Now, we will check the number of solutions of the lines \[r\] and \[s\].
We can observe that the lines \[y - nx = a\sqrt {1 + {n^2}} \] and \[y - nx = - a\sqrt {1 + {n^2}} \] are linear equations in two variables.
Rewriting the equations of the lines, we get
\[ - nx + y - a\sqrt {1 + {n^2}} = 0\] and \[ - nx + y + a\sqrt {1 + {n^2}} = 0\]
Comparing \[ - nx + y - a\sqrt {1 + {n^2}} = 0\] to the standard form \[{a_1}x + {b_1}y + {c_1} = 0\], we get
\[{a_1} = - n\], \[{b_1} = 1\], and \[{c_1} = - a\sqrt {1 + {n^2}} \]
Comparing \[ - nx + y + a\sqrt {1 + {n^2}} = 0\] to the standard form \[{a_2}x + {b_2}y + {c_2} = 0\], we get
\[{a_2} = - n\], \[{b_2} = 1\], and \[{c_2} = a\sqrt {1 + {n^2}} \]
Now, we will find the ratios of the coefficients of \[x\], \[y\], and the constant.
Dividing \[{a_1} = - n\] by \[{a_2} = - n\], we get
\[\dfrac{{{a_1}}}{{{a_2}}} = \dfrac{{ - n}}{{ - n}} = 1\]
Dividing \[{b_1} = 1\] by \[{b_2} = 1\], we get
\[\dfrac{{{b_1}}}{{{b_2}}} = \dfrac{1}{1} = 1\]
Dividing \[{c_1} = - a\sqrt {1 + {n^2}} \] by \[{c_2} = a\sqrt {1 + {n^2}} \], we get
\[\Rightarrow \dfrac{{{c_1}}}{{{c_2}}} = \dfrac{{ - a\sqrt {1 + {n^2}} }}{{a\sqrt {1 + {n^2}} }} = - 1\]
Therefore, we can observe that \[\Rightarrow \dfrac{{{a_1}}}{{{a_2}}} = \dfrac{{{b_1}}}{{{b_2}}} \ne \dfrac{{{c_1}}}{{{c_2}}}\].
Therefore, the lines \[ - nx + y - a\sqrt {1 + {n^2}} = 0\] and \[ - nx + y + a\sqrt {1 + {n^2}} = 0\] have no solution.
This means that the lines \[r\] and \[s\] are parallel lines.
We can show this in the form of a diagram.
 

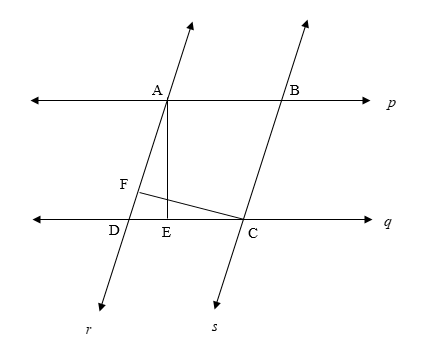
Here, the quadrilateral formed by the 4 lines is a parallelogram, since the opposite pairs of sides are parallel.
Now, we will find the two altitudes of the parallelogram.
The distance between two parallel lines \[ax + by + {c_1} = 0\] and \[ax + by + {c_2} = 0\] is given by the formula \[d = \dfrac{{\left| {{c_2} - {c_1}} \right|}}{{\sqrt {{a^2} + {b^2}} }}\].
The distance between the parallel lines \[p\] and \[q\] is the altitude AE.
Since the lines \[p\] and \[q\], that is \[ - mx + y - a\sqrt {1 + {m^2}} = 0\] and \[ - mx + y + a\sqrt {1 + {m^2}} = 0\] are parallel lines, we get the distance between them as
\[AE = \dfrac{{\left| {a\sqrt {1 + {m^2}} - \left( { - a\sqrt {1 + {m^2}} } \right)} \right|}}{{\sqrt {{{\left( { - m} \right)}^2} + {1^2}} }}\]
Simplifying the expression, we get
\[ \begin{array}{l} AE = \dfrac{{\left| {a\sqrt {1 + {m^2}} + a\sqrt {1 + {m^2}} } \right|}}{{\sqrt {{m^2} + 1} }}\\ \Rightarrow AE = \dfrac{{\left| {a\sqrt {1 + {m^2}} + a\sqrt {1 + {m^2}} } \right|}}{{\sqrt {{m^2} + 1} }}\end{array}\]
Further simplifying the expression, we get
\[\begin{array}{l} \Rightarrow AE = \dfrac{{\left| {2a\sqrt {1 + {m^2}} } \right|}}{{\sqrt {{m^2} + 1} }}\\ \Rightarrow AE = \left| {2a} \right|\\ \Rightarrow AE = 2a\end{array}\]
The distance between the parallel lines \[r\] and \[s\] is the altitude CF.
Since the lines \[r\] and \[s\], that is \[ - nx + y - a\sqrt {1 + {n^2}} = 0\] and \[ - nx + y + a\sqrt {1 + {n^2}} = 0\] are parallel lines, we get the distance between them as
\[CF = \dfrac{{\left| {a\sqrt {1 + {n^2}} - \left( { - a\sqrt {1 + {n^2}} } \right)} \right|}}{{\sqrt {{{\left( { - n} \right)}^2} + {1^2}} }}\]
Simplifying the expression, we get
\[\Rightarrow
 \begin{array}{l} CF = \dfrac{{\left| {a\sqrt {1 + {n^2}} + a\sqrt {1 + {n^2}} } \right|}}{{\sqrt {{n^2} + 1} }}\\ \Rightarrow CF = \dfrac{{\left| {a\sqrt {1 + {n^2}} + a\sqrt {1 + {n^2}} } \right|}}{{\sqrt {{n^2} + 1} }}\\\end{array}\]
After simplification on the expression, we get
\[ \begin{array}{l} CF = \dfrac{{\left| {2a\sqrt {1 + {n^2}} } \right|}}{{\sqrt {{n^2} + 1} }}\\ \Rightarrow CF = \left| {2a} \right|\\ \Rightarrow CF = 2a\end{array}\]
Now, the area of a parallelogram is the product of its base and the altitude on the base.
Thus, we get
Area of parallelogram ABCD \[ = CD \times AE\]
Also, using the altitude CF, we get
Area of parallelogram ABCD \[ = AD \times CF\]
Thus, we get
\[CD \times AE = AD \times CF\]
Substituting \[AE = 2a\] and \[CF = 2a\] in the equation, we get
\[ \Rightarrow CD \times 2a = AD \times 2a\]
Simplifying the expression, we get
\[ \Rightarrow CD = AD\]
We know that if any two adjacent sides of a parallelogram are equal, the parallelogram is a rhombus.
Therefore, since \[CD = AD\], we get that ABCD is a rhombus.
Thus, the correct option is option (b).

Note: We can also prove that the lines \[p,q\] and \[r,s\] are not parallel before drawing the figure, because it can be possible that all the four lines are parallel and no quadrilateral is formed.
Comparing line \[p\], that is \[ - mx + y - a\sqrt {1 + {m^2}} = 0\] to the standard form \[{a_1}x + {b_1}y + {c_1} = 0\], we get
\[{a_1} = - m\], \[{b_1} = 1\], and \[{c_1} = - a\sqrt {1 + {m^2}} \]
Comparing line \[s\], that is \[ - nx + y + a\sqrt {1 + {n^2}} = 0\] to the standard form \[{a_2}x + {b_2}y + {c_2} = 0\], we get
\[{a_2} = - n\], \[{b_2} = 1\], and \[{c_2} = a\sqrt {1 + {n^2}} \]
Dividing \[{a_1} = - m\] by \[{a_2} = - m\], we get
\[\dfrac{{{a_1}}}{{{a_2}}} = \dfrac{{ - m}}{{ - n}} = \dfrac{m}{n}\]
Dividing \[{b_1} = 1\] by \[{b_2} = 1\], we get
\[\dfrac{{{b_1}}}{{{b_2}}} = \dfrac{1}{1} = 1\]
Since \[\dfrac{{{a_1}}}{{{a_2}}} \ne \dfrac{{{b_1}}}{{{b_2}}}\], we have proved that the lines \[p\] and \[s\] have unique solution, and thus are intersecting lines.
Since \[p,q\] are parallel, and \[r,s\] are parallel, the lines \[p,q\] are intersecting with lines \[r,s\].
Thus, our drawn figure is correct.