Question

The straight line $3x + y = 9$ divides the line segment joining the points $\left( {1,3} \right)$ and $\left( {2,7} \right)$ in the ratio:
(A) $3:4$ externally
(B) $3:4$ internally
(C) $4:5$ internally
(D) $5:6$ externally

Answer 1

Hint: In the given question, we are required to find the ratio in which a line divides the join of two points whose coordinates are given to us. Firstly, we find the coordinates of a point at which the line divides the line segment joining the two given points. Then, we find out the ratio in which the join of the two points is divided. The required task can be done using the section formula where we can use a predefined formula given the coordinates of the end points of the line segment and the coordinates of the point at which the line divides the join of endpoints.

Complete step-by-step solution:
We are given the points $\left( {1,3} \right)$ and $\left( {2,7} \right)$.
We find out the equation of the line passing through these two points.
We know the two point form of the line, where we can find the equation of a straight line given the coordinates of two points lying on it. The two point form of the line can be represented as: \[\left( {y - {y_1}} \right) = \dfrac{{\left( {{y_2} - {y_1}} \right)}}{{\left( {{x_2} - {x_1}} \right)}}\left( {x - {x_1}} \right)\] where $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ are the coordinates of the two points.
So, the equation of the line passing through $\left( {1,3} \right)$ and $\left( {2,7} \right)$ is \[\left( {y - 3} \right) = \dfrac{{\left( {7 - 3} \right)}}{{\left( {2 - 1} \right)}}\left( {x - 1} \right)\].
Now, simplifying the equation of the straight line, we get,
\[ \Rightarrow \left( {y - 3} \right) = \dfrac{4}{1}\left( {x - 1} \right)\]
Opening the brackets, we get,
\[ \Rightarrow y - 3 = 4x - 4\]
Shifting the terms, we get,
\[ \Rightarrow y = 4x - 1\]
Now, the equation of the other line is $3x + y = 9$.
Now, we find the point of intersection of these two lines by solving the equations of both.
Substituting the value of y from equation \[y = 4x - 1\] into the equation $3x + y = 9$, we get,
$ \Rightarrow 3x + \left( {4x - 1} \right) = 9$
Simplifying the equation, we get,
$ \Rightarrow 7x = 9 + 1$
Isolating the terms consisting of x, we get,
$ \Rightarrow x = \dfrac{{10}}{7}$
Now, substituting the value of x in the equation $3x + y = 9$, we get,
$ \Rightarrow 3\left( {\dfrac{{10}}{7}} \right) + y = 9$
Opening the bracket, we get,
$ \Rightarrow \dfrac{{30}}{7} + y = 9$
$ \Rightarrow y = 9 - \dfrac{{30}}{7}$
Simplifying the calculations, we get,
$ \Rightarrow y = \dfrac{{63 - 30}}{7}$
$ \Rightarrow y = \dfrac{{33}}{7}$
So, the coordinates of the point at which the line $3x + y = 9$ divides the join of $\left( {1,3} \right)$ and $\left( {2,7} \right)$ are $\left( {\dfrac{{10}}{7},\dfrac{{33}}{7}} \right)$.
Now, we have to find the ratio in which the join of the endpoints $\left( {1,3} \right)$ and $\left( {2,7} \right)$ is divided at the point $\left( {\dfrac{{10}}{7},\dfrac{{33}}{7}} \right)$.
So, let the ratio in which the point $\left( {\dfrac{{10}}{7},\dfrac{{33}}{7}} \right)$ divides the line segment be $k:1$.

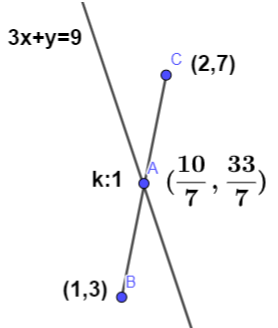
Using section formula, Coordinates of point P \[ = \left( {\dfrac{{n{x_1} + m{x_2}}}{{m + n}},\dfrac{{n{y_1} + m{y_2}}}{{m + n}}} \right)\], where $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ are the coordinates of the endpoints of the line segment and $m:n$ is the ratio in which the Point P divides the line segment.
So, Coordinates of Point P \[ = \left( {\dfrac{{k\left( 1 \right) + 1\left( 2 \right)}}{{k + 1}},\dfrac{{1\left( 7 \right) + k\left( 3 \right)}}{{k + 1}}} \right)\]
Opening the brackets and simplifying the calculations, we get,
\[ = \left( {\dfrac{{k + 2}}{{k + 1}},\dfrac{{3k + 7}}{{k + 1}}} \right)\]
Now, equating this with the actual coordinates of Point P found already, we get,
\[\dfrac{{k + 2}}{{k + 1}} = \dfrac{{10}}{7}\] and \[\dfrac{{3k + 7}}{{k + 1}} = \dfrac{{33}}{7}\]
Cross multiplying the terms in both the equations, we get,
\[ \Rightarrow 7\left( {k + 2} \right) = 10\left( {k + 1} \right)\] and \[ \Rightarrow 7\left( {3k + 7} \right) = 33\left( {k + 1} \right)\]
\[ \Rightarrow 7k + 14 = 10k + 10\] and \[ \Rightarrow 21k + 49 = 33k + 33\]
Shifting the terms, we get,
\[ \Rightarrow 14 - 10 = 10k - 7k\] and \[ \Rightarrow 49 - 33 = 33k - 21k\]
\[ \Rightarrow 4 = 3k\] and \[ \Rightarrow 16 = 12k\]
Now, finding the value of x, we get,
\[ \Rightarrow k = \left( {\dfrac{3}{4}} \right)\]
Hence, the value of k comes out to be \[\left( {\dfrac{3}{4}} \right)\] from both the equations. Also, the division is internal since the ratio came out to be positive.
Hence, the ratio in which the join of the points $\left( {1,3} \right)$ and $\left( {2,7} \right)$ is divided by the line $3x + y = 9$ is $3:4$ internally.

Note: We must remember the section formula and its applications in order to solve the problem. We should understand the language of the question carefully as without understanding the problem, one might not be able to solve it properly. We should know how to solve equations of two given straight lines by substitution method to tackle the problem.