Question

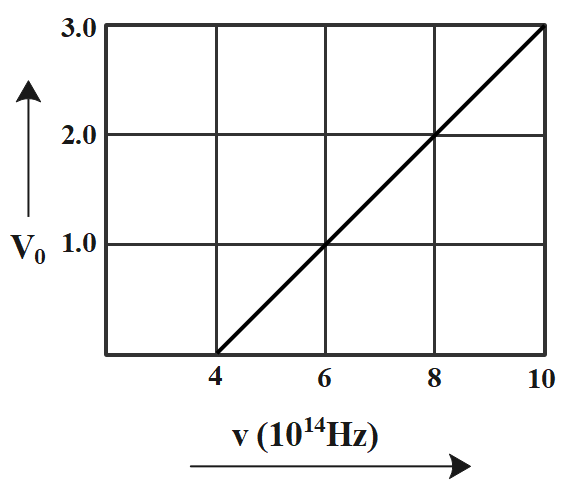
The stopping potential ${V_ \circ }$ (in volt) as a function of frequency (v) for a sodium emitter, is shown in the figure. The work function of sodium, from the data plotted in the figure will be:
(Given: Planck’s constant (h) =6.63$ \times {10^{ - 34}}$Js, electron charge= 1.6$ \times {10^{ - 19}}$ C)

(A) 1.95 eV
(B) 1.82 eV
(C) 1.66 eV
(D) 2.12 eV

Answer 1

Hint: The stopping potential, also known as the stopping voltage is defined as the difference required to stop electrons from moving between plates and creating a current in the photoelectric experiment. On the other hand, the minimum amount of energy required to eject an electron from the metal surface is known as work function. With the help of these two concepts, we solve this problem. We need to study this from the graph given.

Formula used:
hv = $\phi $ + e${v_0}$

Complete solution Step-by-Step:
Einstein gave the equation of photo-electric effect as follows:
hv = $\phi $ + e${v_0}$
where v is the applied frequency .
$\phi $ is the work function .
${v_0}$ is the frequency of the emitted electrons.
Work function is characteristic of the material from which photoelectrons are ejected.
By studying the graph given to us in question, we have,
The incident frequency, v = 4$ \times {10^{14}}$ hz
Also, ${v_0}$= 0 when v = 4$ \times {10^{14}}$ hz.
Plugging the values of ${v_0}$ and v in the photoelectric equation given by Einstein we have,
hv = $\phi $ + e${v_0}$
$\eqalign{
  & \Rightarrow h \times 4 \times {10^{14}} = \phi \cr
  & \Rightarrow 6.626 \times {10^{ - 34}} \times 4 \times {10^{14}} = \phi \cr
  & \therefore 26.504 \times {10^{ - 20}} = \phi \cr} $
Thus in units of joule, the work function is obtained as $26.504 \times {10^{ - 20}}$.
To convert in units of eV, we have to divide this number by 1.6$ \times {10^{ - 19}}$ which is the electronic charge.
Hence, in units of eV, we have the value as = $\dfrac{{26.504 \times {{10}^{ - 20}}}}{{1.6 \times {{10}^{ - 19}}}}$ eV
$\therefore \phi = {\text{ }}1.66{\text{ }}eV$

Thus the correct answer for the value of stopping potential is given as (C)1.66 eV.

Additional Information:
The formula used to calculate the value of stopping potential is the same formula for whose deductions’ Einstein was awarded the Nobel Prize in Physics. The photoelectric effect is a very famous and simple experiment which leads to the evolution of Quantum Mechanics.

Note: In this problem, we must keep in mind the terms stopping potential and work function and what they actually mean in a graph and also mathematically. With these simple concepts, this problem can be solved easily in one go. All problems relating to photoelectric effect can be solved by this same formula given by Einstein.