Question

The steps of construction of an $\angle AOB={{45}^{\circ }}$ is given in jumbled order below:
1. Place compass on intersection point.
2. Place ruler on start point and where arc intersects perpendicular line.
3. Adjust compass width to reach start point.
4. Construct a perpendicular line.
5. Draw a 45-degree line.
6. Draw an arc that intersects a perpendicular line.
The third step in process is:
(a) 2
(b) 3
(c) 4
(d) 5

Answer 1

Hint: We must first read all instructions carefully, and decide the order of occurrence of these instructions. We must also remember the fact that the sum of all interior angles of a triangle is equal to ${{180}^{\circ }}$. After finding the correct order, we must select the third instruction or the third step.

Complete step by step answer:
We need to create an angle AOB measuring ${{45}^{\circ }}$ using a compass and a ruler.
So, we must first construct a perpendicular line on the base of the angle. In the figure shown below, the horizontal line is the base of our angle. The point A is the point of intersection of the horizontal line and the perpendicular line.

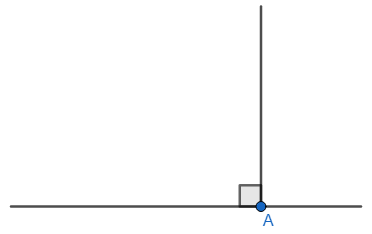
So, number 4 is the first instruction.
Now, we will place the compass on the intersection point A. Thus, the instruction number 1 is the second instruction.
Now, with the compass needle of intersection point A, we will adjust the compass width to reach the starting point. Let this starting point be O. Our figure will look something like the one shown below.

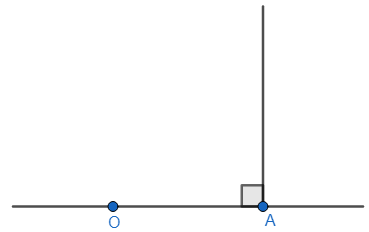
So, instruction number 3 is the third instruction.
We should, now, draw an arc starting from the starting point O and cutting the perpendicular line. Let us assume that the point where this arc intersects the perpendicular line be B. The figure will now become as we have shown below.

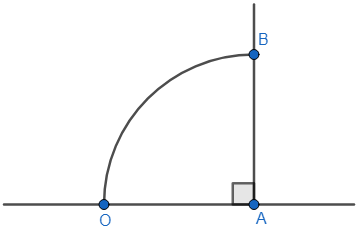
So, we can say that instruction 6 is the fourth instruction.
Now, we must place a ruler such that we can make a line joining the starting point O and the point where the arc intersects the perpendicular line, that is, B. Hence, the instruction number 2 will be the fifth instruction.
And finally, we must draw a line joining the points O and B.

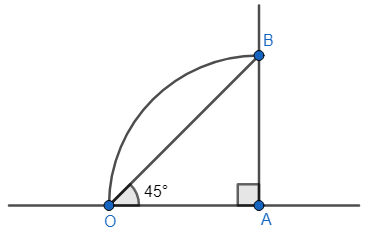
Since OA is equal to AB as both are the radius of this arc and one angle is a right angle, we can say that $\angle AOB=\angle OBA={{45}^{\circ }}$. Thus, the line OB is the ${{45}^{\circ }}$ line. Hence, instruction number 5 is the sixth instruction.
Thus, we can say that the correct sequence of instruction is 4-1-3-6-2-5.
Hence, instruction number 3 is the third step.
So, the correct answer is “Option b”.

Note: We must keep in mind that the sum of all internal angles of a triangle is ${{180}^{\circ }}$. This is the reason for $\angle AOB=\angle OBA={{45}^{\circ }}$. We must note that this is not the commonly used method that we use, in which we bisect the right angle to get an angle of ${{45}^{\circ }}$.