Question

The status of the points $ \left( {1,5} \right) $ and \[\left( {5,1} \right)\] with respect to the line $ x - y = 0 $ is ……….
Both lie on the same side
both lie on the opposite side
both lie on the side
only one of them lie on the line

Answer 1

Hint: The question can be easily solved by tracing the given line on the coordinate axes and then locating the position of points with respect to it, we just need suitable coordinate points to trace the line.

Complete step by step answer:
Now from the question
Equation of line $ x - y = 0 $
Given points are C $ \left( {1,5} \right) $ and D \[\left( {5,1} \right)\]
Now tracing the given equation of line in the coordinate axis by using
 $ \begin{gathered}
  x - y = 0 \\
   \Rightarrow x = y \\
\end{gathered} $
Now making coordinate table for tracing the line
\[\begin{array}{*{20}{c}}
  x&{ - 2}&{ - 1}&0&1&2&3&4 \\
  y&{ - 2}&{ - 1}&0&1&2&3&4
\end{array}\]
Now the line $ x - y = 0 $ is traced in coordinate axis

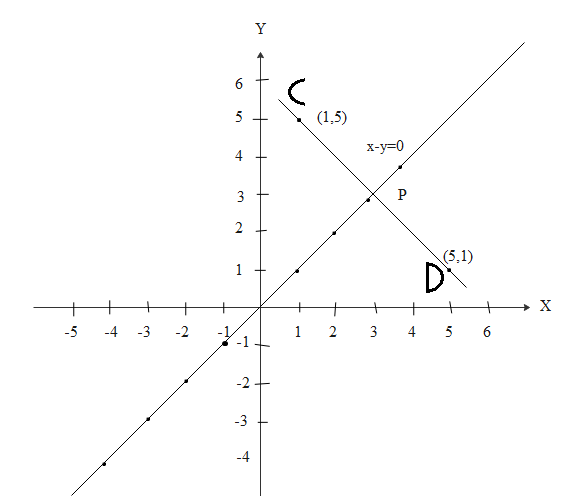
When the points C $ \left( {1,5} \right) $ and D \[\left( {5,1} \right)\] are located in the coordinate axes, they are found to be situated on opposite sides of the line $ x - y = 0 $ . Described clearly in figure.

Hence the correct option is (B)

Note:
 The equation of line formed by the points which intersects a line internally . let C $ \left( {{x_1},{y_1}} \right) $ and D $ \left( {{x_2},{y_2}} \right) $ are on the opposite sides of the line ax + by + c = 0, then the point P on the line ax + by + c = 0 divides the line internally in the ratio $ {m_1}:{m_2} $ , where $ \dfrac{{{m_1}}}{{{m_2}}} $ must be positive.
The Co-ordinates of P are given by
 $ \left( {\dfrac{{{m_1}{x_2} + {m_2}{x_1}}}{{{m_1} + {m_2}}},\dfrac{{{m_1}{y_2} + {m_2}{y_1}}}{{{m_1} + {m_2}}}} \right) $
Point P lies on the line ax + by + c = 0.
 $ \dfrac{{{m_1}}}{{{m_2}}} = \dfrac{{a{x_1} + b{y_1} + c}}{{a{x_2} + b{y_2} + c}} > 0 $
If $ a{x_1} + b{y_1} + c $ and $ a{x_2} + b{y_2} + c $ have same signs as that of ax +by + c then $ \dfrac{{{m_1}}}{{{m_2}}} $ = –ve, so that the point on the line ax + by + c = 0 will divide the line externally in the ratio $ {m_1}:{m_2} $ and the points C $ \left( {{x_1},{y_1}} \right) $ and D $ \left( {{x_2},{y_2}} \right) $ are lying on the same side of the line ax + by + c = 0