Question

The statement $\sim \left( p\leftrightarrow \sim q \right)$ is
\[\begin{align}
  & A.\text{ equivalent to p}\leftrightarrow \text{q} \\
 & \text{B}\text{. equivalent to }\sim \text{p}\leftrightarrow \text{q} \\
 & \text{C}\text{. a tautology} \\
 & \text{D}\text{. a fallacy} \\
\end{align}\]

Answer 1

Hint: To solve this question, we will first make truth tables of \[\sim p,\sim \left( p\leftrightarrow \sim q \right),\sim q,p\leftrightarrow q\text{ and }\sim \text{p}\leftrightarrow \text{q}\] and then to check if given is equivalent to which of the option given, we will match truth tables of all. If all the values of truth tables are equal then, they are equivalent. Also, $\sim p$ denotes 'negation of p' and $p\leftrightarrow q$ denotes p if and only if q.

Complete step by step answer:
Two statements are equivalent if their truth tables have the same value or each entry.
We have if p and q are any statements. Then, $\sim p\Rightarrow \sim q$ denotes negation of p or negation of q. Its truth table is given as:

Again if p and q are two statements then, $p\leftrightarrow q$ denotes p if and only if q. Its truth table is given as:

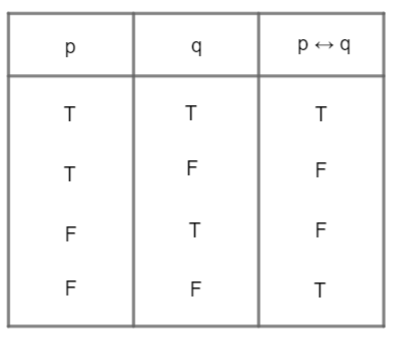
Now, finally we will make truth tables of $\sim \left( p\leftrightarrow \sim q \right)$ then make a truth table of all options and see which one of them matches, then they are equivalent.

So, we have obtained truth table of \[\sim \left( p\leftrightarrow \sim q \right)\]
Now consider option A: $p\leftrightarrow q$ make truth table of $p\leftrightarrow q$

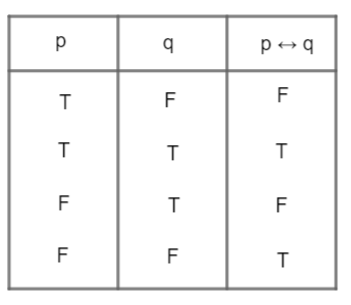
Clearly the truth table of \[\sim \left( p\leftrightarrow \sim q \right)\text{ and }p\leftrightarrow q\] are matching. So, they are equivalent. Hence, option A is correct.
Consider option B: \[\sim p\leftrightarrow q\] make truth table of \[\sim p\leftrightarrow q\]

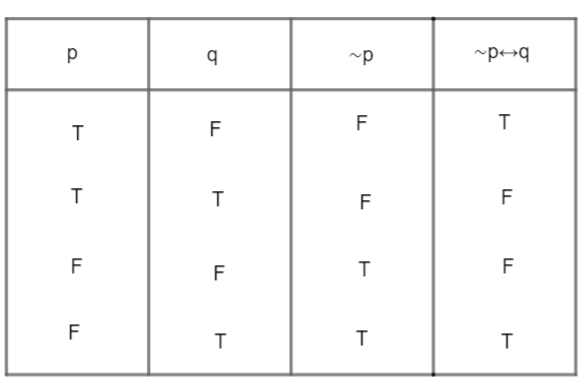
Observing we see that, not all elements of \[\sim p\leftrightarrow q\] matches that of \[\sim \left( p\leftrightarrow \sim q \right)\]
So, \[\sim p\leftrightarrow q\] is not equivalent to \[\sim \left( p\leftrightarrow \sim q \right)\] Hence, option B is wrong.
Consider option C: a tautology. A tautology is a logical statement which has true value at all of its entries of the truth table.
Observing the entries of the truth table of \[\sim \left( p\leftrightarrow \sim q \right)\] we see that, not all entries are true.
So, \[\sim \left( p\leftrightarrow \sim q \right)\] is not a tautology. Hence, option C is wrong.
Consider option D: a fallacy. A fallacy is a logical statement which has false value at all of its entries of the truth table.
Observing the entries of the truth table of \[\sim \left( p\leftrightarrow \sim q \right)\] we see not all entries are “false”.
So, \[\sim \left( p\leftrightarrow \sim q \right)\] is not a fallacy. Hence, option D is wrong.
So, finally we get that \[\sim \left( p\leftrightarrow \sim q \right)\] is equivalent to $p\leftrightarrow q$ so option A is correct.

Note:
The key point to note here in this question is that, $p\leftrightarrow q$ is very different from $\left( p\leftrightarrow \sim q \right)$ So truth table of both:

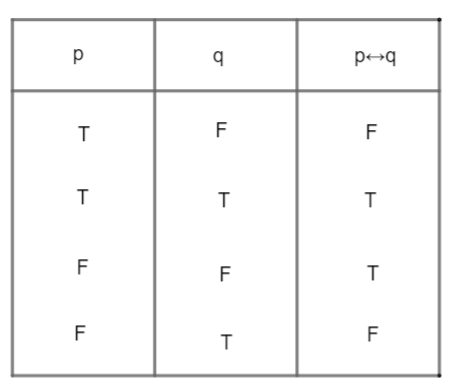
And of $\left( p\leftrightarrow \sim q \right)$ is

So, we observe that value of entries “True or False” change while we apply negation to any statement. $p\leftrightarrow q$ is true if both p and q are either true or are either false. Therefore, applying a negation of $\sim p\Rightarrow \sim q$ changes the value of \[p\leftrightarrow \sim q\Rightarrow \sim p\leftrightarrow q\]