Question

The standard weight of a special purpose brick is 5 kg and it must contain two basic ingredients \[{B_1}\] and ${B_2}$ . \[{B_1}\] costs Rs. 5 per kg and ${B_2}$ costs Rs. 8 per kg. Strength consideration dictate that the brick should contain not more than 4 kg of \[{B_1}\] and minimum 2 kg of ${B_2}$ , Since the demand for the product is likely to be related to the price of the brick, find the minimum cost of brick satisfying the above conditions. Formulate this situation as an LPP and solve it graphically.

Answer 1

Hint: Let us assume that x kg of \[{B_1}\] and y kg of ${B_2}$ is required. It is given that the standard weight of the brick is 5 kg so $x + y = 5$ , then apply the conditions on ingredients as given in question.
After that we have to find the minimum cost of brick satisfying the given conditions.

Complete step-by-step answer:
Let us assume that the weight of basic ingredients ${B_1}\& {B_2}$ in the brick is x kg and y kg respectively.
It is given that the standard weight of the brick is 5 kg so the addition of weight of the basic ingredients ${B_1}\& {B_2}$ is equal to 5.
$x + y = 5$ --- (1)
Now, there is a condition that brick should not contain more than 4 kg of \[{B_1}\] and minimum 2 kg of ${B_2}$ ,
So, we get,
$x \leqslant 4$ -- (2)
$y \geqslant 2$ ---(3)
Now, it is given that \[{B_1}\] costs Rs 5 per kg and ${B_2}$ costs Rs 8 per kg, so total cost is $5x + 8y$
Let us represent this cost function as: $z = 5x + 8y$
We have to minimize z by finding intersection points of equations (1,2&3) on graph paper:

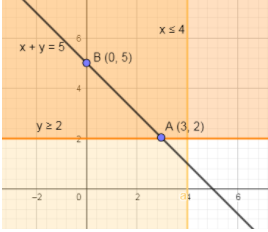
The two points $A(3,2)\& B(0,5)$ are points of intersection.
Substituting these points in cost function, we get,
$z = 5(3) + 8(2) = 15 + 16 = 31$
And $z = 5(0) + 8(5) = 0 + 40 = 40$
From above values, the value of 31 is minimum which is at point (3,2).

Note: The mistake that could happen is in writing inequality in minimum condition. For example: It is given that the minimum weight that ${B_2}$ can have 2 kg means the ingredient should take minimum value 2 and $ \geqslant $ will come for this.