Question

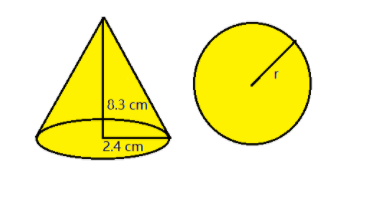
The sphere and cone shown in the diagram have the same volume. Find the radius of the sphere.

Answer 1

Hint:
First of all, calculate the volume of the cone by using the formula \[\dfrac{1}{3}\pi {R^2}h\], where \[R\] is the radius of the cone and \[h\] is the height of the cone. Substitute the values of radius and height in \[\dfrac{1}{3}\pi {R^2}h\] to find the volume of the cone. It is given in the question that the cone and the sphere have the same volume, so equate the calculated volume of the cone to the volume of a sphere, \[\dfrac{4}{3}\pi {r^3}\] and solve the formed equation to find the radius of the sphere, \[r\].

Complete step by step solution:
Given, the radius of cone= 2.4 cm and height of cone= 8.3 cm.
Since the volume of sphere and cone is same, calculate the volume of the cone using the formula, \[\dfrac{1}{3}\pi {R^2}h\], where \[R\] is the radius of the cone and \[h\] is the height of the cone.
When we substitute 2.4 for \[R\], 8.3 for \[h\] and \[\dfrac{{22}}{7}\] for \[\pi \], we obtain the volume as,
$
  V = \dfrac{1}{3}\pi {R^2}h \\
   = \dfrac{1}{3}\left( {\dfrac{{22}}{7}} \right){\left( {2.4} \right)^2}\left( {8.3} \right) \\
$
Now, write the volume of the sphere as after substituting \[\dfrac{{22}}{7}\] for \[\pi \]
$
  V = \dfrac{4}{3}\pi {r^3} \\
  V = \dfrac{4}{3}\left( {\dfrac{{22}}{7}} \right){r^3} \\
$
As, volume of cone and sphere are equal, equate them to find the value of \[r\].
\[\dfrac{4}{3}\left( {\dfrac{{22}}{7}} \right){r^3} = \dfrac{1}{3}\left( {\dfrac{{22}}{7}} \right){\left( {2.4} \right)^2}\left( {8.3} \right)\]
Cancel \[\dfrac{{22}}{7}\] and \[\dfrac{1}{3}\] to simplify the equation.
\[4{r^3} = {\left( {2.4} \right)^2}\left( {8.3} \right)\]
By dividing 4 on both the sides, we get,
$
  {r^3} = \dfrac{{{{\left( {2.4} \right)}^2}\left( {8.3} \right)}}{4} \\
  {r^3} = 11.952 \\
$
When we solve the expression, we get \[r \approx 2.28\]

Hence, the radius of the sphere is approximately 2.28 cm.

Note:
The volume of the sphere is the amount of space that it takes. The volume of the sphere depends on its radius, whereas the volume of the cone depends on its radius and the perpendicular height of the cone. Here, we have to remember the formulas of the volume of the sphere and the volume of the cone.