Question

The speed of a projectile when it is at its greatest height is \[\sqrt{\dfrac{2}{5}}\] times its speed at half the maximum height. What is its angle of projection?

Answer 1

Hint: We need to find the relation of the height of the projectile and the angle of the projectile in a projectile motion in order to find the angle of projection. The equation of the motion in the projectile motion can be used properly to solve this problem.

Complete step-by-step solution
We can use the equation of motion to deduce the velocity of a projectile with an angle of projection \[\theta \] at any height as –
\[\begin{align}
  & {{v}^{2}}-{{(u\cos \theta )}^{2}}=2gh \\
 & \Rightarrow {{v}^{2}}={{u}^{2}}{{\cos }^{2}}\theta +2gh \\
 & \Rightarrow v=\sqrt{{{u}^{2}}{{\cos }^{2}}\theta +2gh} \\
\end{align}\]
We know that the maximum height attained by a projectile is –
\[H=\dfrac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}\]

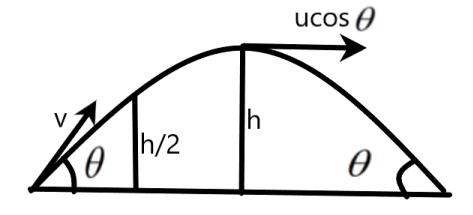
We can substitute the above formula for height in the formula for velocity to get the velocity of the projectile at the maximum height H as –
\[\begin{align}
  & v=\sqrt{{{u}^{2}}{{\cos }^{2}}\theta +2gh} \\
 & \Rightarrow v=\sqrt{{{u}^{2}}{{\cos }^{2}}\theta +2g\dfrac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}} \\
\end{align}\]
But we know that the vertical velocity at the maximum height will be zero. Therefore, we get the velocity at the maximum height to be the horizontal component of the initial velocity ‘u’ as \[u\cos \theta \].
Now, we are to compare the velocities of the projectile at two different heights. The velocity of the projectile at the maximum height is said to be \[\sqrt{\dfrac{2}{5}}\] times the speed of the projectile at the half of the maximum height. We can bring out the equation for this as –
\[{{v}_{H}}=\sqrt{\dfrac{2}{5}}{{v}_{_{\dfrac{H}{2}}}}\]
We can substitute the speed at both the instants in the above equation. We get the relation as –
\[\begin{align}
  & {{v}_{H}}=\sqrt{\dfrac{2}{5}}{{v}_{_{\dfrac{H}{2}}}} \\
 & \Rightarrow u\cos \theta =\sqrt{\dfrac{2}{5}}\sqrt{{{u}^{2}}{{\cos }^{2}}\theta +2gh} \\
\end{align}\]
The half of the maximum height can be given as –
\[{{H}_{\dfrac{1}{2}}}=\dfrac{{{u}^{2}}{{\sin }^{2}}\theta }{4g}\]
We get the angle of projection from substituting all these as –
\[\begin{align}
  & {{v}_{H}}=\sqrt{\dfrac{2}{5}}{{v}_{_{\dfrac{H}{2}}}} \\
 & \Rightarrow u\cos \theta =\sqrt{\dfrac{2}{5}}\sqrt{{{u}^{2}}{{\cos }^{2}}\theta +2g{{H}_{\dfrac{1}{2}}}} \\
 & \Rightarrow u\cos \theta =\sqrt{\dfrac{2}{5}}\sqrt{{{u}^{2}}{{\cos }^{2}}\theta +2g\dfrac{{{u}^{2}}{{\sin }^{2}}\theta }{4g}} \\
 & \Rightarrow {{u}^{2}}{{\cos }^{2}}\theta =\dfrac{2}{5}\sqrt{{{u}^{2}}{{\cos }^{2}}\theta +\dfrac{{{u}^{2}}{{\sin }^{2}}\theta }{2}} \\
 & \Rightarrow 5{{u}^{2}}{{\cos }^{2}}\theta =2{{u}^{2}}{{\cos }^{2}}\theta +{{u}^{2}}{{\sin }^{2}}\theta \\
 & \Rightarrow 4{{\cos }^{2}}\theta =1 \\
 & \Rightarrow {{\cos }^{2}}\theta =\dfrac{1}{4} \\
 & \Rightarrow \cos \theta =\pm \dfrac{1}{2} \\
 & \therefore \theta =\dfrac{\pi }{3}={{60}^{0}} \\
\end{align}\]
The angle of projection of the projectile is therefore, \[{{60}^{0}}\].

Note: The angle of projection is the main factor, which determines the range, time, and height of a projectile for a given initial velocity. We use this theory in many practical cases like in sports and games to get a favorable outcome with the available velocity.