Question

The solution of $\dfrac{3\sin \theta -\sin 3\theta }{1+\cos \theta }+\dfrac{3\cos \theta +\cos 3\theta }{1-\sin \theta }=4\sqrt{2}\cos \left( \theta +\dfrac{\pi }{4} \right)$
A. $n\pi $
B. $n\pi +\dfrac{\pi }{12}$
C. $n\pi \pm \dfrac{\pi }{2}$
D. $2n\pi $

Answer 1

Hint: First we will expand the term $\cos \left( \theta +\dfrac{\pi }{4} \right)$ by using the formula $\cos \left( A+B \right)=\cos A.\cos B-\sin A.\sin B$. Now we will substitute the value $\cos \dfrac{\pi }{4}=\sin \dfrac{\pi }{4}=\dfrac{1}{\sqrt{2}}$ and simplify the term in the right side of the given equation. Now in the left side we have the terms $\sin 3\theta $, $\cos 3\theta $. So we will use the formulas $\sin 3\theta =3\sin \theta -4{{\sin }^{3}}\theta $ and $\cos 3\theta =4{{\cos }^{3}}\theta -3\cos \theta $ then we will simplify the terms in the right side and equate the obtained value to the simplified form of the right side term. Now we will solve the obtained equation to get the result.

Complete step-by-step answer:
Given that,
$\dfrac{3\sin \theta -\sin 3\theta }{1+\cos \theta }+\dfrac{3\cos \theta +\cos 3\theta }{1-\sin \theta }=4\sqrt{2}\cos \left( \theta +\dfrac{\pi }{4} \right)$
Expanding the term $\cos \left( \theta +\dfrac{\pi }{4} \right)$ by using the formula $\cos \left( A+B \right)=\cos A.\cos B-\sin A.\sin B$, then we will get
$\Rightarrow \dfrac{3\sin \theta -\sin 3\theta }{1+\cos \theta }+\dfrac{3\cos \theta +\cos 3\theta }{1-\sin \theta }=4\sqrt{2}\left[ \cos \theta .\cos \dfrac{\pi }{4}-\sin \theta .\sin \dfrac{\pi }{4} \right]$
Now substituting the value $\cos \dfrac{\pi }{4}=\sin \dfrac{\pi }{4}=\dfrac{1}{\sqrt{2}}$ in the above equation, we will get
$\begin{align}
  & \Rightarrow \dfrac{3\sin \theta -\sin 3\theta }{1+\cos \theta }+\dfrac{3\cos \theta +\cos 3\theta }{1-\sin \theta }=4\sqrt{2}\left[ \cos \theta .\dfrac{1}{\sqrt{2}}-\sin \theta .\dfrac{1}{\sqrt{2}} \right] \\
 & \Rightarrow \dfrac{3\sin \theta -\sin 3\theta }{1+\cos \theta }+\dfrac{3\cos \theta +\cos 3\theta }{1-\sin \theta }=4\sqrt{2}\times \dfrac{1}{\sqrt{2}}\left[ \cos \theta -\sin \theta \right] \\
 & \Rightarrow \dfrac{3\sin \theta -\sin 3\theta }{1+\cos \theta }+\dfrac{3\cos \theta +\cos 3\theta }{1-\sin \theta }=4\left( \cos \theta -\sin \theta \right) \\
\end{align}$
We know that $\sin 3\theta =3\sin \theta -4{{\sin }^{3}}\theta $ and $\cos 3\theta =4{{\cos }^{3}}\theta -3\cos \theta $, so substituting these values in the above equation, then we will have
$\begin{align}
  & \Rightarrow \dfrac{3\sin \theta -\left( 3\sin \theta -4{{\sin }^{3}}\theta \right)}{1+\cos \theta }+\dfrac{3\cos \theta +4{{\cos }^{3}}\theta -3\cos \theta }{1-\sin \theta }=4\left( \cos \theta -\sin \theta \right) \\
 & \Rightarrow \dfrac{4{{\sin }^{3}}\theta }{1+\cos \theta }+\dfrac{4{{\cos }^{3}}\theta }{1-\sin \theta }=4\left( \cos \theta -\sin \theta \right) \\
\end{align}$
Multiplying the term $\dfrac{1-\cos \theta }{1-\cos \theta }$ with $\dfrac{4{{\sin }^{3}}\theta }{1+\cos \theta }$ and $\dfrac{1+\sin \theta }{1+\sin \theta }$ with $\dfrac{4{{\cos }^{3}}\theta }{1-\sin \theta }$ in the above equation, then we will get
$\Rightarrow \dfrac{4{{\sin }^{3}}\theta }{1+\cos \theta }\times \dfrac{1-\cos \theta }{1-\cos \theta }+\dfrac{4{{\cos }^{3}}\theta }{1-\sin \theta }\times \dfrac{1+\sin \theta }{1+\sin \theta }=4\left( \cos \theta -\sin \theta \right)$
Using the formula $\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$ in the above equation, then we will get
$\Rightarrow \dfrac{4{{\sin }^{3}}\theta \left( 1-\cos \theta \right)}{{{1}^{2}}-{{\cos }^{2}}\theta }+\dfrac{4{{\cos }^{3}}\theta \left( 1+\sin \theta \right)}{{{1}^{2}}-{{\sin }^{2}}\theta }=4\left( \cos \theta -\sin \theta \right)$
We have the trigonometric identity ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$, from this identity the values of $1-{{\cos }^{2}}\theta $ and $1-{{\sin }^{2}}\theta $ are ${{\sin }^{2}}\theta $, ${{\cos }^{2}}\theta $ respectively. Substituting these values in the above equation, then we will have
$\begin{align}
  & \Rightarrow \dfrac{4{{\sin }^{3}}\theta \left( 1-\cos \theta \right)}{{{\sin }^{2}}\theta }+\dfrac{4{{\cos }^{3}}\theta \left( 1+\sin \theta \right)}{{{\cos }^{2}}\theta }=4\left( \cos \theta -\sin \theta \right) \\
 & \Rightarrow 4\sin \theta \left( 1-\cos \theta \right)+4\cos \theta \left( 1+\sin \theta \right)=4\left( \cos \theta -\sin \theta \right) \\
\end{align}$
Applying multiplication distribution law in the above equation, then we will get
$\begin{align}
  & \Rightarrow 4\sin \theta -4\sin \theta .\cos \theta +4\cos \theta +4\cos \theta .\sin \theta =4\cos \theta -4\sin \theta \\
 & \Rightarrow 4\sin \theta +4\cos \theta -4\cos \theta +4\sin \theta =0 \\
 & \Rightarrow 8\sin \theta =0 \\
 & \Rightarrow \sin \theta =0 \\
\end{align}$
We know that the solution for the equation $\sin \theta =0$ is given by $\theta =n\pi $.
Hence the solution for the given equation is $\theta =n\pi $.

So, the correct answer is “Option A”.

Note: We can also solve the problem by drawing the equation in graph. When we solve the given equation, we get the equation $\sin \theta =0$ so draw a graph for the $\sin \theta =0$ as shown in the figure below.

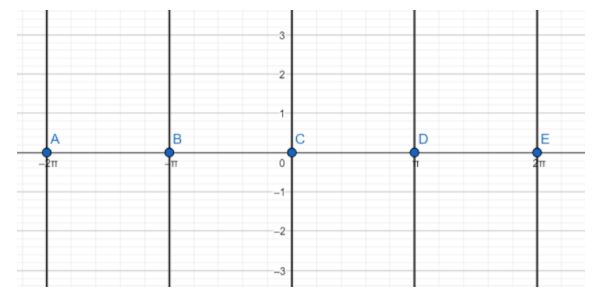
Here we can clearly observe that the equation has zero value for $\theta =\pm \pi ,\pm 2\pi ,\pm 3\pi ,...$. We can simply write it as $\theta =n\pi $. From both the methods we got the same result.