Question

The slope of the windscreen of the two cards are ${\alpha _1} = {30^ \circ }$and ${\alpha _2} = {15^ \circ }$respectively. At what ratio $\dfrac{{{v_1}}}{{{v_2}}}$ of the velocities of the cars will their drivers see the hailstones bounced by the windscreen on their cards in the vertical direction. Assume hailstones fall vertically downwards and collisions to be elastic.
A. 3
B. 2
C. 1
D. $\dfrac{1}{2}$

Answer 1

Hint: In this problem, the main concept required is the concept of elastic collision. Elastic collision is defined as the situation where the kinetic energies of the two colliding bodies remain the same after colliding with each other. In other words, the net mechanical energy in the system of collision of two bodies remains the same before and after the collision.

Complete step-by-step answer:
Consider the diagram of the windshield being hit by a hailstone on car 1:

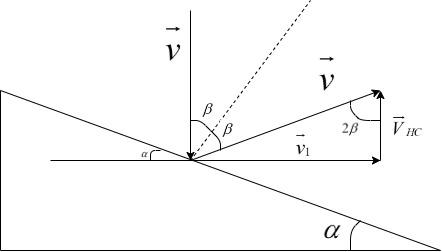
Here, $\overrightarrow v $ is the velocity of the hailstorm. Since, it is mentioned that the collision is elastic, the velocity of the hailstone after colliding with the windshield remains the same and it makes an angle $2\beta $ with the initial velocity direction before collision.
Now, the velocity $\overrightarrow v $ after collision, can be resolved into two components as shown in the figure, such that :
Since the vector $\overrightarrow v $ makes a right angle with the direction of $\overrightarrow {{v_1}} $, observing the figure, we can write the following equation:
$90 - \alpha = 90 - 2\left( {\beta + \beta } \right) + \beta $
Rearranging, we get –
$\alpha = \beta \to 2\alpha = 2\beta $
In the velocity triangle formed in the figure above,
$\tan 2\beta = \dfrac{{{v_1}}}{{{V_{HC}}}}$
There are two different cars with different angles of windshields here. So, we will consider the angle $\alpha $as ${\alpha _1}$and${\alpha _2}$
Substituting for both of these angles, we get –
$
  \tan 2\beta = \tan 2{\alpha _1} = \dfrac{{{v_1}}}{{{V_{HC}}}} \\
  Similarly, \\
  \tan 2\beta = \tan 2{\alpha _2} = \dfrac{{{v_2}}}{{{V_{HC}}}} \\
 $
From these equations, we can write –
\[\dfrac{{{v_1}}}{{{v_2}}} = \dfrac{{\tan 2{\alpha _1}}}{{\tan 2{\alpha _2}}}\]
Given: ${\alpha _1} = {30^ \circ }$and ${\alpha _2} = {15^ \circ }$
Substituting, we get –
\[
  \dfrac{{{v_1}}}{{{v_2}}} = \dfrac{{\tan 2{\alpha _1}}}{{\tan 2{\alpha _2}}} \\
  \dfrac{{{v_1}}}{{{v_2}}} = \dfrac{{\tan 2 \times 30}}{{\tan 2 \times 15}} = \dfrac{{\tan 60}}{{\tan 30}} \\
   \to \dfrac{{{v_1}}}{{{v_2}}} = \dfrac{{\sqrt 3 }}{{\dfrac{1}{{\sqrt 3 }}}} = {\left( {\sqrt 3 } \right)^2} = 3 \\
 \]
Therefore, the ratio of the velocities \[\dfrac{{{v_1}}}{{{v_2}}} = 3\]

Hence, the correct option is Option A.

Note: In this problem, for the vector addition, we have used the triangle law of addition.
The triangle law of addition of vectors states that – If there are two vectors in the same order, the resultant of the vectors is the closing side of the triangle formed but of the opposite order.

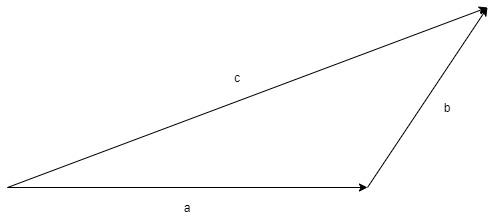
As per the triangle law of addition, we have –
$\overrightarrow c = \overrightarrow a + \overrightarrow b $