Question

The slope of the graph between $ \log p $ and $ \log V $ at constant temperature for a given mass of a gas is:
(A) $ +1 $
(B) $ -1 $
(C) $ 1/T $
(D) $ 1/n $

Answer 1

Hint :We know that according to Boyle’s law, for a given mass of a gas, the pressure is inversely proportional to volume occupied by that gas at a constant temperature. From this information, a relationship between $ \log p $ and $ \log V $ can be easily established for the given conditions. Formula Used: $ {{p}_{1}}{{V}_{1}}={{p}_{2}}{{V}_{2}} $ .

Complete Step By Step Answer:
According to Boyle’s law:
 $ p\propto 1/V $ , for constant number of moles, $ n $ at constant temperature, $ T $
We can say that, $ p=c/V $ , where $ c $ is a constant.
 $ \Rightarrow pV=c $ (constant).
Taking logarithms of both sides, we get:
 $ \log pV=\log c $ .
Applying the formula, $ \log mn=\log m+\log n $ :
 $ \log p+\log V=\log c $ .
Rearranging the above equation:
 $ \log p=-\log V+\log c $ .
Here, $ \log p $ and $ \log V $ are variables and $ \log c $ is a constant.
Comparing the above equation with $ y=mx+C $ , we get:
 $ y=\log p $ , $ m=-1 $ , $ x=\log V $ and constant $ C=\log c $ .
Here, $ m $ is the slope between the graph of $ y $ and $ x $ .
Therefore, the slope of the graph between $ \log p $ and $ \log V $ at constant temperature for a given mass of a gas is equal to $ -1 $ .
The following slope graph is given as:

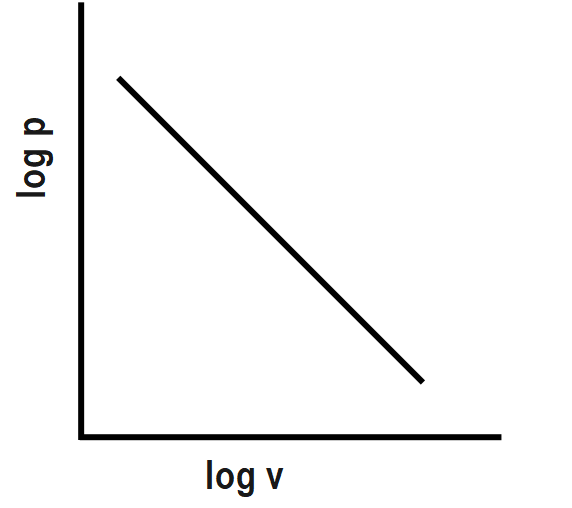
Hence, option (B) is the correct answer.

Note :
Remember that Boyle’s law holds good for an ideal gas. Gases are at high temperature and low pressures behave near to ideal gas. Here, we have assumed that the given gas behaves as an ideal gas. Therefore, the required slope can also be found out by using the ideal gas equation, $ pV=nRT $ .
Taking logarithms of both sides, we get:
 $ \log pV=\log nRT $ .
Here, $ n $ , $ R $ and $ T $ are constant, thus:
 $ \log p+\log V=\text{constant} $ .
Rearranging the above equation:
 $ \log p=-\log V+\text{constant} $ .
Hence, we get the same value of slope, $ m=-1 $ .