Question

The slant height of a conical mountain is \[2.5\,km\] and the area of its base \[1.54\,k{m^2}\] . Find the height of the mountain

Answer 1

Hint: The question is related to the geometry topic, since it is the word problem, the data can be recognized by reading the sentences. So first by the area of the base we determine the length of the side and then by using the Pythagoras theorem we determine the value of height of the mountain.

Complete step-by-step solution:
This is a word problem, so by reading the question we will write the given data. The below diagram will represents the clear picture of the question

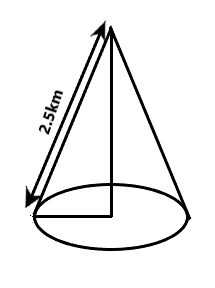
The slant height of a mountain = \[2.5\,km\] and the slant height is represented by l
The area of the base of the mountain = \[1.54\,k{m^2}\]
The area of the base of a mountain is in the form of a circle.
The area of the circle’s formula is given by \[A = \pi {r^2}\]
On substituting the value of the area of base we can determine the value of radius.
 \[ \Rightarrow 1.54 = \pi {r^2}\]
The value of \[\pi \] is given as \[\dfrac{{22}}{7}\], on substituting in above equation we have
\[ \Rightarrow 1.54 = \dfrac{{22}}{7}{r^2}\]
On multiplying by 7 on both sides we get
\[ \Rightarrow 1.54 \times 7 = \dfrac{{22}}{7} \times 7{r^2}\]
\[ \Rightarrow 10.78 = 22{r^2}\]
On dividing the above equation by 22 we get
\[ \Rightarrow {r^2} = 0.49\]
Taking square root on both sides we get
\[ \Rightarrow r = 0.7km\]
We are considering a positive value because the distance can’t be negative.
On considering the diagram

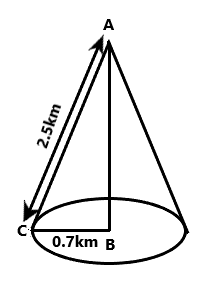
The \[\vartriangle ABC\] is a right-angled triangle, so we can use the Pythagoras theorem.
\[ \Rightarrow A{C^2} = A{B^2} + B{C^2}\]
On substituting the known values
\[ \Rightarrow {(2.5)^2} = {h^2} + {(0.7)^2}\]
Here h represents the height of a mountain
\[ \Rightarrow 6.25 = {h^2} + 0.49\]
On taking 0.49 to LHS we get
\[ \Rightarrow 6.25 - 0.49 = {h^2}\]
On simplifying we get
\[ \Rightarrow {h^2} = 5.76\]
On taking square root on both sides we get
\[ \Rightarrow h = 2.4\]
We are considering a positive value because the distance can’t be negative.
Therefore the height of the mountain is \[2.4km\].

Note: In a word problem the student should read each sentence, because each sentence will contain the data which is required to solve the given problem. The selection of arithmetic operations or formulas is also dependent on the sentence in the question. Since we are determining the height we have to mention the unit.