Question

The slant height and base diameter of a conical tomb are 25m and 14m respectively. Find the cost of white-washing its curved surface at the rate of 210 per 100sq.m.

Answer 1

Hint: Curved surface area of cone is given as $\pi rl$ where $\pi =\dfrac{22}{7}$ , ‘r’ is representing the radius and ‘l’ is slant height of the cone. Now, find the cost with the given rate of white washing.

Complete step-by-step answer:
Here, we have a conical tomb with slant height as 25m and base diameter is given as 14m. So, we need to determine the cost of white washing its curved surface area at the rate of Rs.210 per $100{{m}^{2}}$. Hence, first of all, we need to calculate curved surface area and hence the cost as well.
So, we can represent the given conical tomb as

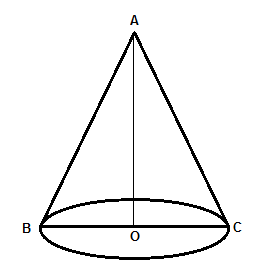
We know the formula to calculate the curved surface area of the cone would be given as
$S=\pi rl..............\left( i \right)$
Where: S = Surface area, $\pi =\dfrac{22}{7}$, r = radius of cone, l = Slant height of the cone.
So, we know the value of ‘r’ and ‘l’ as $\dfrac{14}{2}$ or 7m and 25m respectively from the information provided in the problem.
Hence, curved surface area of the conical tomb can be given from equation (i) as
$\begin{align}
  & S=\dfrac{22}{7}\times 7\times 25 \\
 & S=22\times 25 \\
 & S=550{{m}^{2}} \\
\end{align}$
 Now, we know the cost of white washing $100{{m}^{2}}$is 210 Rs.
So, with the help of unitary method, we get to know the cost of white washing $1{{m}^{2}}$ area which is $\dfrac{210}{100}\text{Rs}\text{.}$
Hence, the cost for white washing the conical tomb can be given as,
$\dfrac{210}{100}\times 550=21\times 55$
Cost = 1155 Rs.
Hence, the cost of white-washing its curved surface at the rate of 210 per 100sq.m is Rs.1155/-.

Note: One can use the formula of calculating curved surface area as $\pi rl+\pi {{r}^{2}}$ , which is wrong. As here we are adding base area as well. So, it’s representing total surface area.
Don’t confuse the terms slant height and height in cone. In the figure, AO is representing height and AB is slant height.
One may multiply the curved surface area calculated by the conical tomb directly with 210, which will be wrong. As cost Rs.210 is not representing $1{{m}^{2}}$, it’s for $100{{m}^{2}}$ .