Question

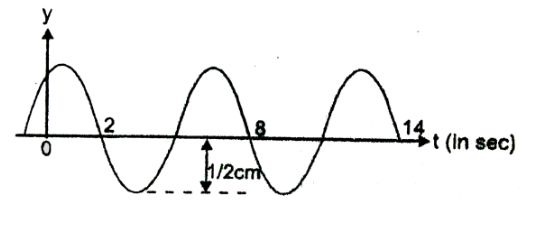
The sketch in the figure shows the displacement time curve of a sinusoidal wave at $ x = 8m $ . Taking the velocity of the wave $ v = 6m{s^{ - 1}} $ along the positive X-axis, write the equation of the wave.
(A) $ y = 0.5\sin \left( {\dfrac{\pi }{3}t + \dfrac{\pi }{{18}}x + \dfrac{{7\pi }}{9}} \right) $
(B) $ y = 0.5\sin \left( {\dfrac{\pi }{3}t + \dfrac{\pi }{{18}}x + \dfrac{{11\pi }}{9}} \right) $
(C) $ y = 0.5\sin \left( {\dfrac{\pi }{3}t - \dfrac{\pi }{{18}}x + \dfrac{{11\pi }}{9}} \right) $
(D) $ y = 0.5\sin \left( {\dfrac{\pi }{3}t - \dfrac{\pi }{{18}}x + \dfrac{{7\pi }}{9}} \right) $

Answer 1

Hint :Use the general equation of a sinusoidal wave and find the different parameters of the wave. The general equation of a sinusoidal wave propagating along positive X-direction is given by, $ y = A\sin \left( {\omega t - kx + \varphi } \right) $ . Where, $ A $ is the amplitude of the wave, $ \omega $ is the angular frequency of the wave, $ k $ is the propagation constant of the wave, $ \varphi $ is the initial phase, $ x $ is the position of the wave and $ t $ is the time.

Complete Step By Step Answer:
We know that the equation of a sinusoidal wave propagating along positive X- direction is given by, $ y = A\sin \left( {\omega t - kx + \varphi } \right) $ . Where, $ A $ is the amplitude of the wave, $ \omega $ is the angular frequency of the wave, $ k $ is the propagation constant of the wave, $ \varphi $ is the initial phase. $ x $ is the position of the wave and $ t $ is the time.
From the figure we can see that at $ t = 2s $ to $ t = 8s $ the wave completes one single oscillation. Now we know, the time period of a wave is the time required to complete one complete oscillation is called the time period of the wave. Hence the time period of the wave will be, $ T = (8 - 2) = 6s $ .
Now, we know that the frequency of a wave is the total number of complete oscillation in one second.
Hence, frequency of the wave will be, $ f = \dfrac{1}{T} = \dfrac{1}{6}Hz $ .
So, the angular frequency of the wave will be, $ \omega = 2\pi f $ .
Putting the values we get, $ \omega = 2\pi \dfrac{1}{6} = \dfrac{\pi }{3}rad/s $
Now, From the figure we can see that the amplitude of the wave is , $ A = 0.5cm = 5 \times {10^{ - 3}}m $ .
Now we know that the propagation constant of the wave is related to the wavelength of the wave as, $ k = \dfrac{{2\pi }}{\lambda } $ . And we know, wavelength of wave is the distance covered in one complete oscillation , $ \lambda = \dfrac{v}{f} $ where $ v $ is the velocity of the wave.
We have given here that the velocity of the wave is, $ v = 6m{s^{ - 1}} $ and we have found $ f = \dfrac{1}{6}Hz $ .
Putting the values we get, $ \lambda = \dfrac{6}{{\dfrac{1}{6}}} = 36m $ .
Hence propagation constant will be, $ k = \dfrac{{2\pi }}{\lambda } = \dfrac{{2\pi }}{{36}} = \dfrac{\pi }{{18}}{m^{ - 1}} $
So, putting these values in the sinusoidal wave equation we get the wave equation as,
 $ y = 0.5\sin \left( {\dfrac{\pi }{3}t - \dfrac{\pi }{{18}}x + \varphi } \right) $ [Taking displacement in $ cm $ ]
Since, there is insufficient data to find the initial phase of the wave we have to check the available options.
Now, putting, $ \varphi = \dfrac{{11\pi }}{9} $ at $ t = 0 $ and $ x = 8 $
we get, $ y = 0.5\sin (0 - \dfrac{{8\pi }}{{18}} + \dfrac{{11\pi }}{9}) $
Or, $ y = 0.5\sin (\dfrac{{7\pi }}{9}) = 0.321 $
So, putting $ \varphi = \dfrac{{7\pi }}{9} $ at $ t = 0 $ and $ x = 8 $
We get, $ y = 0.5\sin (0 - \dfrac{{8\pi }}{{18}} + \dfrac{{7\pi }}{9}) $
Or, $ y = 0.5\sin (\dfrac{\pi }{3}) = 0.433 $
From observation of the graph we can see that the value of $ y $ t $ t = 0 $ and $ x = 8 $ must be near the $ y \geqslant 0.4cm $ range. Hence, $ \varphi = \dfrac{{7\pi }}{9} $ must be the initial phase.
So, equation of the wave will be, $ y = 0.5\sin \left( {\dfrac{\pi }{3}t - \dfrac{\pi }{{18}}x + \dfrac{{7\pi }}{9}} \right) $
So, Option (D) is correct.

Note :
 $ \bullet $ Here, if the value of the amplitude of the wave at $ t = 0s $ was given we could find the initial phase of the wave directly.
 $ \bullet $ The equation of standing waves always has a fixed value of $ x $ . The figure of the wave given here is a standing wave since, only the variation of the displacement of the wave with time is given at $ x = 8m $ , but it is not actually a standing wave since it is told that the wave is propagating along the positive X-axis.