Question

The simplest rationalising factor of $\sqrt[4]{{48}}$ is
A) $\sqrt[4]{9}$
B) $\sqrt[4]{{27}}$
C) $\sqrt[3]{9}$
D) None of these

Answer 1

Hint: By the word rationalizing we get a strike in our mind, what is the value of a function needed to multiply and divide. Which is eventfully equal to 1 to remove the root. Here we will rationalise 48 to get the actual value under the root by taking out the maximum possible, to multiply it with its inverse to get a whole number.

Complete step by step solution: As we go, step by step. First, we need to factories the inner value is $\sqrt[4]{{48}}$

So Let’s calculate the factors of 48. Here we are going to use Prime factorization.

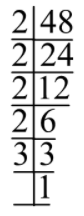
So, we got the factors of 48 as $2 \times 2 \times 2 \times 2 \times 3$ which can also be written as ${2^4} \times 3$

Let’s write the factor in the given form.
i.e $\sqrt[4]{{48}} = \sqrt[4]{{{2^4} \times 3}} = 2\sqrt[4]{3}$
Here, we need to rationalize the factor $\sqrt[4]{3}$ get a whole no without any root. So, let’s find out what needs to be multiplied and get rid of the root.

to get $\sqrt[4]{3}$ as 3, we need to multiply $\sqrt[4]{{{3^3}}}$

Let’s multiply and divide with $\sqrt[4]{{{3^3}}}$
$2\sqrt[4]{3} \times \dfrac{{\sqrt[4]{{{3^3}}}}}{{\sqrt[4]{{{3^3}}}}} = \dfrac{{2\sqrt[4]{{3 \times {3^3}}}}}{{\sqrt[4]{{{3^3}}}}} = \dfrac{{2 \times \sqrt[4]{{{3^3}}}}}{{\sqrt[4]{{{3^3}}}}} = \dfrac{6}{{\sqrt[4]{{{3^3}}}}}$
So, we got a rational number by multiplying $\sqrt[4]{{{3^3}}} = \sqrt[4]{{37}}$ with $\sqrt[4]{{48}}$

Hence, Rationalizing factor of $\sqrt[4]{{48}}$ is$\sqrt[4]{{27}}$ .

Option B is the correct option.

Note: Always try to factorise and get all the values out of root to get minimal value in the root to rationalize. One fascinating fact is every number can be expressed as some powers of prime numbers. It’s one of the vastly used facts in abstract algebra.