Question

The sides of triangle are in the ratio 4:6:7 then
A.The triangle is obtuse angled triangle
B.The triangle is acute angled triangle
C.The triangle is right angled triangle
D.The triangle is impossible

Answer 1

Hint: In this problem we have to use what are the exact conditions for a triangle to be either acute, obtuse or right angle. If a, b, c are the three sides of a triangle then,
1.For an acute angle triangle: \[{a^2} + {b^2} > {c^2}\]
2.For an obtuse angle triangle: \[\dfrac{{{c^2}}}{2} < {a^2} + {b^2} < {c^2}\]
3.For a right angle triangle: \[{a^2} + {b^2} = {c^2}\]

Complete step-by-step answer:
 As we have mentioned conditions for different triangles above in the hint lets test.
Here a: b: c is 4:6:7

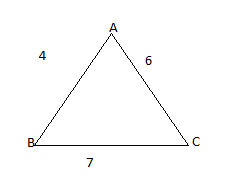
So,
\[
  {a^2} = {4^2} = 16 \\
  {b^2} = {6^2} = 36 \\
  {c^2} = {7^2} = 49 \\
\]
Now
\[{a^2} + {b^2} = 16 + 36 = 52\]
And \[{c^2} = 49\]
Thus \[{a^2} + {b^2} > {c^2}\] is the only condition satisfied.
So the given triangle is an acute angle.
So option B is correct.

Note: Since we have mentioned the conditions for the triangles don’t judge the condition of obtuse angle from one side only .Both should be satisfied. And for right angles the given ratio of numbers does not satisfy the condition.