Question

The sides of an equilateral triangle ABC are 12 cm each , D is the foot of the perpendicular from A to BC and E is the midpoint of AD. Then BE is
A.$4\sqrt 3 $cm
B.$6\sqrt 2 $cm
C.$\sqrt {63} $cm
D.None of these

Answer 1

Hint: Since we are given an equilateral triangle ABC and AD is perpendicular to BC. By using the property the height of an equilateral triangle bisects its base we get BD=6cm and then by using Pythagoras theorem we can find AD and then considering the small triangle BDE and using Pythagoras theorem we can find BE

Complete step-by-step answer:
Given ABC is an equilateral triangle .
Hence all its sides are equal.

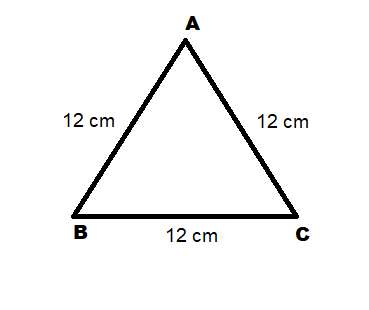
And it's also given that D is the foot of the perpendicular from A to BC
It means that AD is perpendicular to BC

Step 2 :
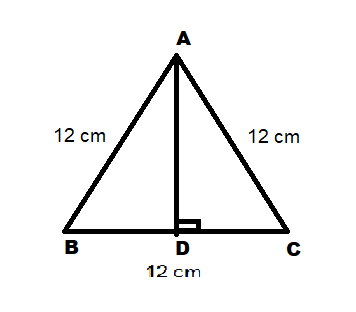
Since ABC is an equilateral triangle , we know that the height or altitude of an equilateral triangle bisects its base.
Here AD is the height of the triangle .
Therefore it bisects the base and now we have BD=BC=6cm
Step 3:
Now let's find AD by using Pythagoras theorem
Consider the triangle ABD . It is a right triangle .

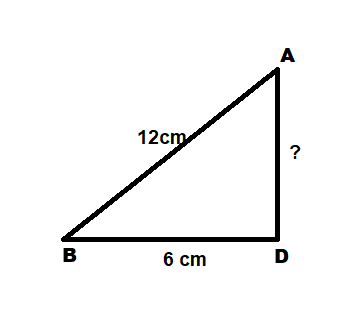
By using Pythagoras theorem
$
   \Rightarrow {({\text{Hypotenuse }})^2} = {\text{ Sum of squares of other two sides}} \\
   \Rightarrow {\left( {AB} \right)^2} = {\left( {AD} \right)^2} + {\left( {BD} \right)^2} \\
   \Rightarrow {12^2} = {\left( {AD} \right)^2} + {6^2} \\
   \Rightarrow 144 = {\left( {AD} \right)^2} + 36 \\
   \Rightarrow 144 - 36 = {\left( {AD} \right)^2} \\
   \Rightarrow 108 = {\left( {AD} \right)^2} \\
   \Rightarrow AD = \sqrt {108} \\
$
Now we have that $AD = \sqrt {108} cm$
Step 4 :
We are given that E is the midpoint of AD.

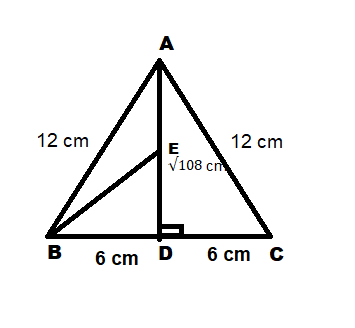
Since E is the midpoint of AD , we have AE=ED=$\frac{{\sqrt {108} }}{2}$cm
We need to find BE , so let's consider the right triangle BDE
Lets use Pythagoras theorem to find BE
 \[
   \Rightarrow {({\text{Hypotenuse }})^2} = {\text{ Sum of squares of other two sides}} \\
   \Rightarrow {\left( {BE} \right)^2} = {\left( {ED} \right)^2} + {\left( {BD} \right)^2} \\
   \Rightarrow {\left( {BE} \right)^2} = {\left( {\frac{{\sqrt {108} }}{2}} \right)^2} + {6^2} \\
   \Rightarrow {\left( {BE} \right)^2} = \frac{{108}}{4} + 36 \\
    \\
\]
Now by taking lcm we get
$
   \Rightarrow {\left( {BE} \right)^2} = \frac{{108 + 144}}{4} \\
   \Rightarrow {\left( {BE} \right)^2} = \frac{{252}}{4} \\
   \Rightarrow {\left( {BE} \right)^2} = 63 \\
   \Rightarrow BE = \sqrt {63} cm \\
$
Therefore $BE = \sqrt {63} cm$
The correct option is C

Note: The sides of an equilateral triangle are congruent.
An equilateral triangle is a special case of a triangle where all 3 sides have equal length and all 3 angles are equal to 60 degrees.