Question

The sides of a triangular field are in the ratio 5:3:4 and its perimeter is 180 meters. Find:
(i) Its area
(ii) Altitude of the triangle corresponding to its largest side
(iii) The cost of levelling the field at the rate of Rs.10 per square meter

Answer 1

Hint: In this question, we need to evaluate the area of the triangle, altitude of the triangle corresponding to largest side and the cost of levelling the field at the rate of Rs.10 per square meter such that the sides of a triangular field are in the ratio 5:3:4 and its perimeter is 180 meters. For this, we will first calculate the sides of the triangle and then use Heron's formula to get the area, use the Pythagoras theorem to get the length of the altitude corresponding to its largest side and then multiply the area by 10 to get the cost of levelling the field.

Complete step-by-step answer:
Let the common multiplier be ‘x’.
According to the question, the length of the sides are in the ratio of 5:3:4 then, the sides of the triangle are given as 5x, 3x and 4x.
Also, it has been given that the perimeter of the triangle is 180 meters so,
 $
  5x + 3x + 4x = 180 \\
   \Rightarrow 12x = 180 \\
   \Rightarrow x = \dfrac{{180}}{{12}} \\
   \Rightarrow x = 15 \\
  $
Hence, the length of the sides of the triangle are
 $
  5x = 5 \times 15 = 75 \\
  3x = 3 \times 15 = 45 \\
  4x = 4 \times 15 = 60 \\
  $
(i)Now, using Heron's formula to evaluate the area of the triangle as
 $ A = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $ where, a, b, and c are the length of the sides of the triangles and $ s = \dfrac{{a + b + c}}{2} $ .
So,
 $
  s = \dfrac{{a + b + c}}{2} \\
   = \dfrac{{75 + 45 + 60}}{2} \\
   = \dfrac{{180}}{2} \;
   = 90 \\
  $
Substituting the value of ‘s’ in the formula $ A = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $ we get,
\[
  A = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} \\
   = \sqrt {90\left( {90 - 75} \right)\left( {90 - 45} \right)\left( {90 - 60} \right)} \\
   = \sqrt {21 \times 15 \times 45 \times 30} \\
   = \sqrt {425250} \\
   = 652.11 \;
 \]
Hence, the area of the triangle is 652.11 square meters.
So, the correct answer is “652.11 sq.m”.

(ii)According to our calculations, the following pictorial representation of the triangle has been made.
Let ‘h’ be the height of the altitude corresponding to the longest side of the triangle.

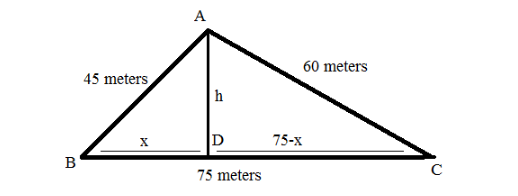
Applying Pythagoras theorem in the triangle ABD, we get
 $
  {\left( {AB} \right)^2} = {\left( {BD} \right)^2} + {\left( {AD} \right)^2} \\
   \Rightarrow {45^2} = {x^2} + {h^2} \\
   \Rightarrow 2025 = {x^2} + {h^2} - - - - (i) \\
  $
Again, applying Pythagoras theorem in the triangle ADC, we get
 $
  {\left( {AC} \right)^2} = {\left( {DC} \right)^2} + {\left( {AD} \right)^2} \\
   \Rightarrow {60^2} = {\left( {75 - x} \right)^2} + {h^2} \\
   \Rightarrow 3600 = 5625 + {x^2} - 150x + {h^2} - - - - (ii) \\
  $
Substituting the value from the equation (i) to the equation (ii) we get
 $
  3600 = 5625 + {x^2} - 150x + {h^2} \\
   \Rightarrow 5625 - 3600 + 2025 = 150x \\
   \Rightarrow 150x = 4050 \\
   \Rightarrow x = \dfrac{{4050}}{{150}} \\
   \Rightarrow x = 27 \;
  $
Substituting the value of ‘x’ in the equation (i), we get
 $
  2025 = {\left( {27} \right)^2} + {h^2} \\
   \Rightarrow {\left( h \right)^2} = 2025 - 729 \\
   \Rightarrow {\left( h \right)^2} = 1296 \\
   \Rightarrow h = \sqrt {1296} \\
   \Rightarrow h = 36 \;
  $
Hence, the altitude is 36 meters.
So, the correct answer is “36 m”.

(iii)Multiplying the area of the triangle by 10, we get the cost of levelling the field at the rate of Rs.10 per square meter.
 $
  {\text{Cost}} = 652.11 \times 10 \\
   = 6521.1 \;
  $
Hence, the cost of labelling the triangular field is Rs.6521.1.
So, the correct answer is “RS.6521.1”.

Note: It is very interesting to note here that we have used almost all the formulae related to the triangle such as Herons formula for the calculations of the area, Pythagoras theorem for the calculation of the altitude and concept of perimeter to determine the length of the sides of the triangular field. These formulae are very general and could be used in many of the questions.