Question

The sides of a triangle have lengths $11, 15$ and $k$ where $k$ is an integer. For how many values of $k$ is the triangle obtuse?

Answer 1

Hint:
By using the triangle laws, that is nothing but, the sum of two sides of the triangle should always be greater than the third side and the modulus difference of two sides will be less than the third side. By using this law we can get the range of values for $k$ which makes the triangle obtuse.

Complete step by step solution:
First we need to know when a triangle is obtuse?
According to the law of cosine, a triangle is said to be obtuse when the sum of the squares of the two sides of a triangle is less than the square of the third side or we can also say the square of a side should be greater than the sum of squares of other two sides.

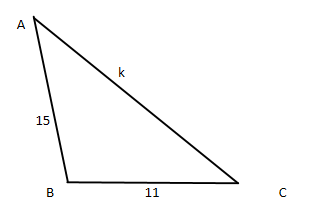
Let us assume the triangle as in the above diagram.
First, we take 15 as the greater value in the triangle. By using cosine law as stated above we can write
${15^2} > {11^2} + {k^2}$
$ \Rightarrow 225 > 121 + {k^2}$
$ \Rightarrow 225 - 121 > {k^2}$
$ \Rightarrow 104 > {k^2}$ or ${k^2} < 104$
Taking square root on both the side, we get
$k < \sqrt {104} $ or $k < 10.19$ …….(1)
Now, by using triangle inequality law, which states that sum of two sides is always greater than third side, we can write $11 + k > 15$
$ \Rightarrow k > 15 - 11$
$ \Rightarrow k > 4$ …….(2)
By comparing equation (1) and (2) the values of $k$will be
$k = 5,6,7,8,9,10$.
Now, we take k in the bigger side of the triangle, so by using cosine rule we can write as
${k^2} > {15^2} + {11^2}$
$ \Rightarrow {k^2} > 225 + 121$
$ \Rightarrow {k^2} > 346$
Taking square root on both sides, we get
$ \Rightarrow k > \sqrt {346} $ or $ \Rightarrow k > 18.6$ …….(3)
Now, by using triangle equality law, which states that sum of two sides is always greater than third side, we can write $11 + 15 > k$
$ \Rightarrow 26 > k$ or $k > 26$ ………(4)
By comparing equation (3) and (4) the values of $k$ will be as follows
$k = 19,20,21,22,23,24,25$
Therefore, the values of $k$ can be $k = 5, 6, 7, 8, 9, 10, 19, 20, 21, 22, 23, 24, 25$.

Hence, the number of values of $k$ is $13$.

Note:
By using triangle laws we can find a range of values, though some of the numbers in the same range may not form the triangle obtuse, so by making use of cosine rule along with triangle law if we solve then we end up with the correct answer.