Question

The sides of a triangle are $3cm$, $5cm$ and $4cm$. Its area is:
A). $6c{m^2}$
B). $7.5c{m^2}$
C). $5\sqrt 2 c{m^2}$
D). None of these

Answer 1

Hint: We are given that the lengths of the three sides of a triangle are $3cm$, $5cm$ and $4cm$. So, for finding the area of the triangle we will use Heron’s formula. According to Heron’s formula area of a triangle whose sides are of length $a$, $b$ and $c$ units is given as: $Area = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $ , here $'s'$ is the semi-perimeter of the triangle as $s = \dfrac{{a + b + c}}{2}$ .
Formula: $Area = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $ and $s = \dfrac{{a + b + c}}{2}$

Complete step-by-step solution:
Given: lengths of a triangle are $3cm$, $5cm$ and $4cm$.

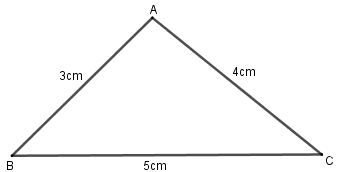
Let $a = 3cm$, $b = 5cm$ and $c = 4cm$.
So, the perimeter of the triangle will be:
$s = \dfrac{{3 + 5 + 4}}{2}cm$
$ \Rightarrow s = \dfrac{{12}}{2}cm$
$ \Rightarrow s = 6cm$
As we know area of a triangle whose lengths of all three sides are known is given as:
$Area = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} .......\left( i \right)$
We have,
$s = 6cm$, $a = 3cm$, $b = 5cm$ and $c = 4cm$.
Substitute all the values in equation $\left( i \right)$
$Area = \sqrt {6\left( {6 - 3} \right)\left( {6 - 5} \right)\left( {6 - 4} \right)} c{m^2}$
After subtraction, we get
$ \Rightarrow Area = \sqrt {6\left( 3 \right)\left( 1 \right)\left( 2 \right)} c{m^2}$
$ \Rightarrow Area = \sqrt {6 \times 3 \times 1 \times 2} c{m^2}$
After multiplication, we get
$ \Rightarrow Area = \sqrt {36} c{m^2}$
The square root of a number can be both positive and negative. But here we have to find an area so we will write only the positive value of square root because the area can’t be negative.
$ \Rightarrow Area = 6c{m^2}$
So, the area of the triangle is $6c{m^2}$.
Hence, option (A) is the correct answer.

Note: Here, by the word semi-perimeter we mean half of the perimeter of the triangle. So, for finding the semi-perimeter we just divide the perimeter by $2$. Students should be careful about the unit. In the given question units are the same but they can be different in any other question. Calculations should be done in the same unit. Write area only in positive value because area can’t be negative as it is the region occupied inside the boundary.