Question

The sides of a square are x = 4, x = 7, y = 1 and y = 4. Then the equation of the circumference of the square is ?
A. ${{x}^{2}}+{{y}^{2}}-11x-5y+32=0$
B. ${{x}^{2}}+{{y}^{2}}-11x-5y+14=0$
C. ${{x}^{2}}+{{y}^{2}}-6x-5y+7=0$
D. None of these

Answer 1

Hint: We will first draw the diagram of the square. Then we will use the concept that the midpoint of diagonals gives the centre of a circle and half of the diagonal equals the radius of the circle that circumscribes the square. We know that if we have the centre (a, b) and the radius r, then the equation of the circle is given by, ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$.

Complete step-by-step answer:
We have been given the sides of a square as, x = 4, x = 7, y = 1 and y = 4 and have been asked to find the equation of the circumference of the square. We will draw the square first with the inputs given in the question.

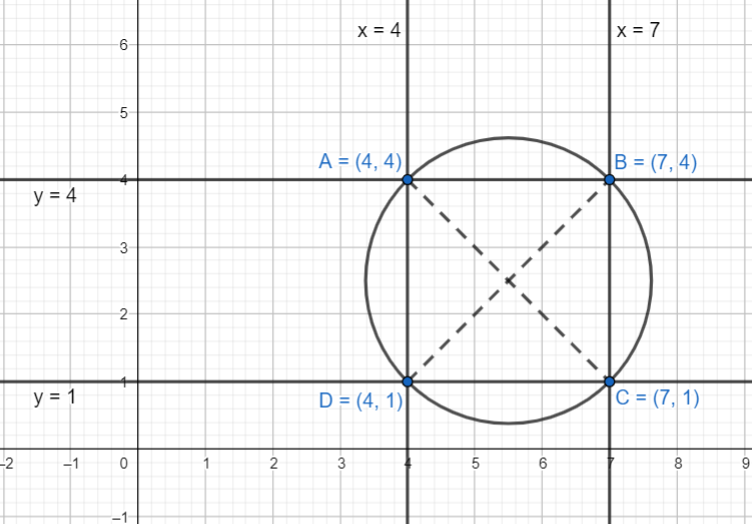
So, we can see from the above figure that we get the required square as ABCD with A (4, 4), B (7, 4), C (7, 1) and D (4, 1). Now, we know that the midpoint of the diagonals of the square gives the centre of the circle that circumscribes it. The midpoint formula is given by, $x=\dfrac{{{x}_{1}}+{{x}_{2}}}{2},y=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}$, where $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ are the two points. Now, we have the two points A (4, 4) and C (7, 1), so we get,
 $\begin{align}
  & x=\dfrac{4+7}{2}=\dfrac{11}{2} \\
 & y=\dfrac{4+1}{2}=\dfrac{5}{2} \\
\end{align}$
We also know that the radius of the circumcircle of the square is equal to half of the length of its diagonal. We know that the distance formula for distance between two points $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ is given by, $D=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$. We have the end points of the diagonals of the square as, A (4, 4) and C (7, 1). Therefore, we get the diagonal AC as,
$\begin{align}
  & AC=\sqrt{{{\left( 4-7 \right)}^{2}}+{{\left( 4-1 \right)}^{2}}} \\
 & \Rightarrow AC=\sqrt{{{3}^{2}}+{{3}^{2}}} \\
 & \Rightarrow AC=\sqrt{9+9} \\
 & \Rightarrow AC=\sqrt{18} \\
 & \Rightarrow AC=3\sqrt{2} \\
\end{align}$
So, we will get the radius of the circumcircle = $\dfrac{3\sqrt{2}}{2}$ units. Now, we have the centre of the circumcircle as $\left( \dfrac{11}{2},\dfrac{5}{2} \right)$ and the radius as $\dfrac{3\sqrt{2}}{2}$ units. We also know that the general equation of a circle having radius r and centre (a, b) is given by ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$. So, we get the equation of the circumcircle as,
$\begin{align}
  & {{\left( x-\dfrac{11}{2} \right)}^{2}}+{{\left( y-\dfrac{5}{2} \right)}^{2}}={{\left( \dfrac{3\sqrt{2}}{2} \right)}^{2}} \\
 & \Rightarrow {{x}^{2}}-11x+\dfrac{121}{4}+{{y}^{2}}-5y+\dfrac{25}{4}=\dfrac{18}{4} \\
\end{align}$
On multiplying the equation by 4, we will get,
$4{{x}^{2}}-44x+121+4{{y}^{2}}-20y+25=18$
On rearranging the terms, we will get,
$\begin{align}
  & 4{{x}^{2}}+4{{y}^{2}}-44x-20y+121+25-18=0 \\
 & \Rightarrow 4{{x}^{2}}+4{{y}^{2}}-44x-20y+128=0 \\
\end{align}$
By taking 4 as common, we will get,
$4\left( {{x}^{2}}+{{y}^{2}}-11x-5y+32 \right)=0$
On dividing the equation by 4, we will get,
${{x}^{2}}+{{y}^{2}}-11x-5y+32=0$
So, we get the equation of the circumference of the square as, ${{x}^{2}}+{{y}^{2}}-11x-5y+32=0$.
Therefore, the correct answer is option A.

Note: We should be careful while doing the calculation as there are chances of making mistakes with the signs, while finding the equation of the circle. We should also remember that we can use the diametric equation form to find the equation of the circumcircle, since AC and BD are the diameters of the circle. It is given by $\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)+\left( y-{{y}_{1}} \right)\left( y-{{y}_{2}} \right)=0$ , where $\left( {{x}_{1}},{{y}_{1}} \right)\text{ }and\text{ }\left( {{x}_{2}},{{y}_{2}} \right)$ can be the coordinates of either A and C or B and D.