Question

The sides of a right triangle are \[a,a + d\;\] and \[a + 2d\], with a and d both positive. The ratio of a to d is:

Answer 1

Hint: We are given 3 sides of a right angled triangle. We start by taking the right angle at the intersection of the smallest and the 2nd smallest line, as the hypotenuse is the largest line in the right angled triangle. Then we use Pythagoras theorem and simplifying it will give us the result.

Complete step-by-step answer:
We are given: Sides of right angled triangle is \[a;a + d;a + 2d\left[ {a,d > 0} \right]\]
We have to find: \[a:d\].
Now we, Let \[AB = a;BC = a + d;CA = a + 2d\]

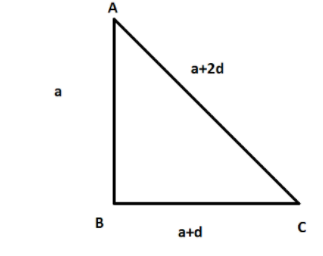
\[\vartriangle ABC\;\] is right angled at B
In \[\vartriangle ABC\;\]
By Pythagoras theorem, we have,
\[A{B^2} + B{C^2} = A{C^2}\]
On substituting values we get,
\[ \Rightarrow {a^2} + {\left( {a + d} \right)^2} = {\left( {a + 2d} \right)^2}\]
On rearranging we get,
\[ \Rightarrow {a^2} = {\left( {a + 2d} \right)^2} - {\left( {a + d} \right)^2}\]
Using, \[\left[ {{a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)} \right]\] , we get
\[ \Rightarrow {a^2} = \left( {a + 2d + a + d} \right)\left( {a + 2d - a - d} \right)\]
On simplification we get,
\[ \Rightarrow {a^2} = \left( {2a + 3d} \right)\left( d \right)\]
On multiplication we get,
\[ \Rightarrow {a^2} = 2ad + 3{d^2}\]
On rearranging we get,

\[ \Rightarrow {a^2} - 2ad = 3{d^2}\]

Adding \[{d^2}\] to both the sides

\[ \Rightarrow {a^2} - 2ad + {d^2} = 3{d^2} + {d^2}\]

Using, \[\left[ {{{\left( {a - b} \right)}^2} = {a^2} - 2ab + {b^2}} \right]\], we get

\[ \Rightarrow {(a - d)^2} = 4{d^2}\]

Taking square root from both sides,

\[ \Rightarrow (a - d) = \pm 2d\]

So, we get,

\[ \Rightarrow a - d = 2d\] or \[ \Rightarrow a - d = - 2d\]

\[ \Rightarrow a = 3d\] or \[ \Rightarrow a = - d\]

\[a = - d\] is not possible as a and d both are positive.

Thus we get,

\[a = 3d\]

\[ \Rightarrow \dfrac{a}{d} = \dfrac{3}{1}\]

\[ \Rightarrow a:d = 3:1\]


Note: Pythagoras theorem states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides“. The sides of this triangle have been named as Perpendicular, Base and Hypotenuse. Here, the hypotenuse is the longest side, as it is opposite to the angle \[90^\circ .\]The sides of a right triangle (say a, b and c) which have positive integer values, when squared, are put into an equation, also called a Pythagorean triplet.