Question

The sides of a rectangle are chosen at random each less than 10cm, all such lengths being equally likely. The chance that the diagonal of the rectangle is less than 10cm is
A.$\dfrac{1}{{10}}$
B.$120$
C.$\dfrac{\pi }{4}$
D.$\dfrac{\pi }{8}$

Answer 1

Hint: We can represent all the rectangles having sides less than 10 cm under the area of the square with 10cm. Then we can represent the rectangles having diagonal less than 10cm as the arc of radius 10cm inside the square. Then we can find the probability by comparing the area of the square and the arc. The area of the square will be the total possibility and the area under the arc will be the favourable outcomes.

Complete step-by-step answer:

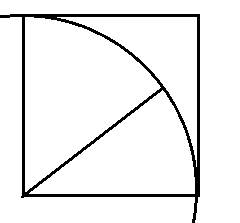
We can draw a square with side 10cm and the arc of the circle with radius 10cm joining the diagonally opposite corners.
All the rectangles having length less than 10 cm will be inside the area of the square of side 10 cm.
We know that the radius of the circle will be equal to every point on the circle from the centre.
As the radius of the arc here is 10cm, all the possible triangles with diagonal less than 10 cm will be inside the area of the quarter of the circle.
We need to choose a rectangle whose side is less than 10cm. Its possibility is given by the area of the square.
Therefore, number of possible outcome is ${a^2} = {10^2}$
The favourable event is that the diagonal of the rectangle is less than 10cm. its possibility comes under the area of the quarter of the circle which is given by $\dfrac{{\pi {r^2}}}{4}$
Therefore, number of favourable outcome is $\dfrac{{\pi {a^2}}}{4} = \dfrac{{\pi \times {{10}^2}}}{4}$
We know that probability of an event is given by the number of favourable outcomes divided by the total number of possible outcomes.
$ \Rightarrow P = \dfrac{{no.\,of\,favourable\,outcomes}}{{no.\,of\,possible\,outcomes}}$
On substituting the values, we get,
$P = \dfrac{{\dfrac{{\pi \times {{10}^2}}}{4}}}{{{{10}^2}}}$
 On simplification, we get,
$ \Rightarrow P = \dfrac{\pi }{4}$
Therefore, the required probability is $\dfrac{\pi }{4}$.
So, the correct answer is option C.
Note: The length of the diagonal of a rectangle with side a and b is given by $\sqrt {{a^2} + {b^2}} $. As both the diagonals of a rectangle are equal, we only need to consider one diagonal. We need not to calculate the actual area as we can cancel the terms while calculating the probability. The area represents all the possible points on the area and each point in the given area will give a rectangle with different length and breadth.