Question

The sides of a quadrangular field taken in order are 26, 27, 7, 24 respectively. The angle contained by the last two sides is a right angle. Find its area.

Answer 1

Hint: Here we are given with the four sides of a quadrangular field. But we are not given the height of the field nor the vertices of the points .So we will divide the field in two triangles and then we will use Heron’s formula and find the areas of the field.

Formula used:
If a, b, c are the three sides of a triangle given then area of the triangle is given by Heron’s formula,
\[S = \dfrac{{Sum{\text{ }}of{\text{ }}all{\text{ }}sides}}{2} = \dfrac{{a + b + c}}{2}\]
Where S is the semi perimeter of the triangle
\[area = \sqrt {S\left( {S - a} \right)\left( {S - b} \right)\left( {S - c} \right)} \]

Complete step-by-step answer:
Let’s draw a diagram of the field first.

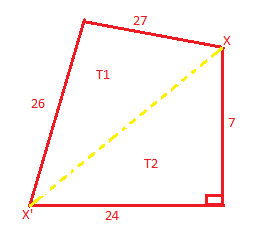
Observe the diagram of the plot above. The diagonal XX’ is dividing the field in two triangles T1 and T2.
It is given that the angle between the last two sides is the right angle. Now using the formula of Pythagoras theorem we will find the diagonal XX’.
\[
   \Rightarrow XX' = \sqrt {{{24}^2} + {7^2}} \\
   \Rightarrow XX' = \sqrt {576 + 49} \\
   \Rightarrow XX' = \sqrt {625} \\
   \Rightarrow XX' = 25 \\
\]
Thus the value of diagonal is found. Now we know all the three sides of the triangle so we can use Heron’s formula to find the value of areas of the triangles.
For T1:
For T1 sides are 26, 27, 25.
\[S = \dfrac{{Sum{\text{ }}of{\text{ }}all{\text{ }}sides}}{2} = \dfrac{{a + b + c}}{2}\]
\[ \Rightarrow S = \dfrac{{26 + 27 + 25}}{2} = \dfrac{{78}}{2} = 39\]
Now to find area,
\[
  Area = \sqrt {S\left( {S - a} \right)\left( {S - b} \right)\left( {S - c} \right)} \\
   \Rightarrow \sqrt {39\left( {39 - 26} \right)\left( {39 - 27} \right)\left( {39 - 25} \right)} \\
   \Rightarrow \sqrt {39 \times 13 \times 12 \times 14} \\
   \Rightarrow \sqrt {85179} \\
   \Rightarrow 291.85uni{t^2} \\
\]
Similarly we will find an area for the second triangle.
For T2:
For T2 sides are 24, 25,7.
\[S = \dfrac{{Sum{\text{ }}of{\text{ }}all{\text{ }}sides}}{2} = \dfrac{{a + b + c}}{2}\]
\[ \Rightarrow S = \dfrac{{24 + 25 + 7}}{2} = \dfrac{{56}}{2} = 28\]
Now to find area,
\[
  area = \sqrt {S\left( {S - a} \right)\left( {S - b} \right)\left( {S - c} \right)} \\
   \Rightarrow \sqrt {28\left( {28 - 24} \right)\left( {28 - 7} \right)\left( {28 - 25} \right)} \\
   \Rightarrow \sqrt {28 \times 4 \times 21 \times 3} \\
   \Rightarrow \sqrt {7056} \\
\]
Hence found the areas of the triangle .Now add them to get the total area of the field.
Total area of the field=
 \[
  T1area + T2area \\
   \Rightarrow 291.85 + 84 \\
   \Rightarrow 375.85uni{t^2} \\
    \\
\]
Note: We can also find the area of T2 by using the formula of base and height. But it is not applicable for T1.
We have taken sides of T2 to find the diagonal because one of its angles is 90 degree.