Question

The sides of a parallelogram is \[2.5\] m longer than its adjacent side. If the perimeter of the parallelogram is \[51\] m, find the measure of all the sides.

Answer 1

Hint: At first, we consider the length of any side of the parallelogram. The adjacent side will be \[2.5\] m longer than the taken side.
Using the formula of the perimeter of a parallelogram, we will find the value of an unknown side. Then we can find the other sides also.

Complete step-by-step answer:
It is given that; the sides of a parallelogram are \[2.5\] m longer than its adjacent side. It is also given that; the perimeter of the parallelogram is \[51\] m.
We have to find the length of all the sides.
Let us consider \[ABCD\] to be a parallelogram.

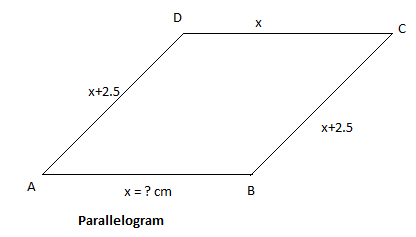
We know that the opposite sides of the parallelogram are equal and parallel.
So, we have \[AB = CD\] and \[AD = BC\].
Let us consider, \[AB = CD = x\] cm
As per the given information \[AD = BC = x + 2.5\] cm
We know that perimeter is the entire length of a figure.
So, we have, the perimeter of the parallelogram is \[AB + BC + CD + AD\].
According to the problem we have,
\[ \Rightarrow AB + BC + CD + AD = 51\]
Substitute the values of the sides we get,
\[ \Rightarrow x + x + x + 2.5 + x + 2.5 = 51\]
Simplifying we get,
\[ \Rightarrow 4x + 5 = 51\]
Simplifying again we get,
\[ \Rightarrow 4x = 51 - 5\]
Simplifying again we get,
\[ \Rightarrow x = \dfrac{{46}}{4}\]
Solving we get,
\[ \Rightarrow x = 11.5\]
So, we have, \[AB = CD = 11.5\] cm
\[ \Rightarrow AD = BC = 11.5 + 2.5 = 14\] cm
Hence, the sides of the parallelogram are \[11.5,{\text{ }}14,{\text{ }}11.5,{\text{ }}14\] cm.

Note: A parallelogram is a quadrilateral with two pairs of parallel sides. The opposite sides of a parallelogram are equal in length, and the opposite angles are equal in measure. Also, the interior angles on the same side of the transversal are supplementary.
The perimeter is the length of the outline of a shape.
Perimeter of a parallelogram is the sum of all the sides of the parallelogram.