Question

The side of the square is 8 cm. Find the length of its diagonal.

Answer 1

Hint: Both the diagonals split the square in two equal right-angled triangles. Using the Pythagoras theorem, we can then find the length of the diagonal as two of the sides are known.
Formula used-
Pythagoras theorem
 $ {H^2} = {P^2} + {B^2} $ where H, P, B are the hypotenuse, perpendicular and base of any right-angled triangle respectively.

Complete step-by-step answer:
We can see in the following diagram of the given square ABCD.
Here we can see that diagonal AC divides the square in two right angled triangles ABC and ACD.

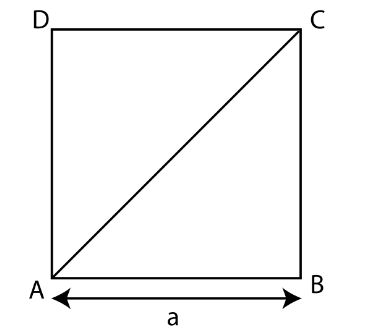
Now, for any right-angled triangle, Pythagoras theorem states that
 $ {H^2} = {P^2} + {B^2} $ where H, P, B are the hypotenuse, perpendicular and base of the triangle. For this question, we can write
 $ {\left( {AC} \right)^2} = {\left( {AB} \right)^2} + {\left( {BC} \right)^2} $
Because this is a square, the sides AB=AC=a, that is given to be 8 cm. Substituting the value in the above equation, we get
 $
  {\left( {AC} \right)^2} = {\left( 8 \right)^2} + {\left( 8 \right)^2} \\
   \Rightarrow {\left( {AC} \right)^2} = 2\times {\left( 8 \right)^2} \\
   \Rightarrow AC = \sqrt {2\times {{\left( 8 \right)}^2}} = 8\sqrt 2\; cm \;
  $
Also, for the second triangle i.e. ACD, applying Pythagoras theorem,
 $
  {\left( {AC} \right)^2} = {\left( {AD} \right)^2} + {\left( {AD} \right)^2} \\
   \Rightarrow {\left( {AC} \right)^2} = {8^2} + {8^2} = {2\times 8^2} \\
   \Rightarrow AC = 8\sqrt 2 \;
  $
Also, if we take BD as diagonal, then it will divide the square in triangles ABD and BCD. Applying the Pythagoras theorem, on triangle ABD
 $
  {\left( {BD} \right)^2} = {\left( {AB} \right)^2} + {\left( {BD} \right)^2} \\
   \Rightarrow {\left( {BD} \right)^2} = {8^2} + {8^2} = {2\times 8^2} \\
   \Rightarrow BD = 8\sqrt 2 \;
  $
Similarly, we can find the length of a diagonal by using triangle BCD. From all upper equations we can notice that basically for any square we can see that the length of the diagonal is $ \sqrt 2 $ times the side of the square.
Therefore, the length of the diagonal of the given square is $ 8\sqrt 2\; cm $ .
So, the correct answer is “$ 8\sqrt 2\; cm $”.

Note: In this question, we can also use the trigonometric ratios to find the length of the diagonal of square.
 $
  \sin 45 = \dfrac{{AB}}{{AC}} = \dfrac{8}{{AC}} \\
   \Rightarrow \dfrac{1}{{\sqrt 2 }} = \dfrac{8}{{AC}} \\
   \Rightarrow AC = 8\sqrt 2 cm \;
  $