Question

The side of a regular hexagon is 2 cm. Then, the ratio of the radius of the circumscribed circle to the radius of the inscribed circle is
(a) \[\dfrac{{\sqrt 3 }}{2}\]
(b) \[\dfrac{1}{2}\]
(c) 2
(d) \[\dfrac{2}{{\sqrt 3 }}\]

Answer 1

Hint:
Here, we will first prove that all the constructed triangles are congruent. Then, we will use the complete angle and the isosceles triangle property to prove that all the six triangles are equilateral. Then, we will use the radius to a tangent property to find the altitude and median of the equilateral triangle. Finally, we will use the Pythagoras’s theorem and simplify the equation to get the ratio of the radius of the circumscribed circle to the radius of the inscribed circle.
Formula Used: We will use the formula for the Pythagoras theorem given by \[{\rm{Hypotenuse}}{{\rm{e}}^2} = {\rm{Bas}}{{\rm{e}}^2} + {\rm{Perpendicular}}{{\rm{r}}^2}\].

Complete step by step solution:
Let the radius of the circumscribed circle and the radius of the inscribed circle be \[R\] and \[r\] respectively.
First, we will draw the figure.

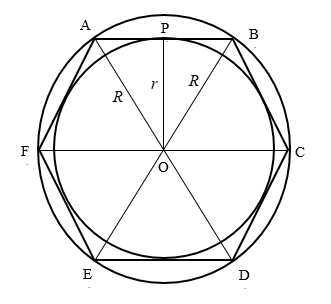
Here, OP is the radius of the inscribed circle, OA, OB, OC, OD, OE, and OF are the radii of the circumscribed circle.
Now, in triangles AOB and BOC, we can observe that
\[AO = BO\] (Radii of the same circle)
\[OB = OC\] (Radii of the same circle)
\[AB = BC = 2\] cm (All sides of a regular hexagon are equal)
Therefore, by S.S.S. congruence criterion, we have proved that the triangles AOB and BOC are congruent.
Since corresponding parts of congruent triangles are equal, we get \[\angle AOB = \angle BOC\].
Similarly, we can prove that all the triangles AOB, BOC, COD, DOE, EOF, FOA are congruent to each other.
Therefore, we get
\[\angle AOB = \angle BOC = \angle COD = \angle DOE = \angle EOF = \angle FOA\]
We know that a complete angle measures 360 degrees.
Therefore, we get
\[\angle AOB + \angle BOC + \angle COD + \angle DOE + \angle EOF + \angle FOA = 360^\circ \]
Using \[\angle AOB = \angle BOC = \angle COD = \angle DOE = \angle EOF = \angle FOA\], we get
\[\begin{array}{l} \Rightarrow \angle AOB + \angle AOB + \angle AOB + \angle AOB + \angle AOB + \angle AOB = 360^\circ \\ \Rightarrow 6\angle AOB = 360^\circ \end{array}\]
Dividing both sides by 6, we get
\[ \Rightarrow \angle AOB = 60^\circ \]
Thus, we get
\[\angle AOB = \angle BOC = \angle COD = \angle DOE = \angle EOF = \angle FOA = 60^\circ \]
Now, in triangle AOB, AO and BO are equal, being the radii of the same circle. Also we know that the angles opposite to equal sides of a triangle are equal.
Therefore, since \[AO = BO\], we get
\[\angle OAB = \angle OBA\]
Now, we will use the angle sum property of a triangle.
Using the angle sum property of a triangle in triangle AOB, we get
\[ \Rightarrow \angle OAB + \angle OBA + \angle AOB = 180^\circ \]
Substituting \[\angle OAB = \angle OBA\] and \[\angle AOB = 60^\circ \] in the equation, we get
\[\begin{array}{l} \Rightarrow \angle OAB + \angle OAB + 60^\circ = 180^\circ \\ \Rightarrow 2\angle OAB + 60^\circ = 180^\circ \end{array}\]
Subtracting \[60^\circ \] from both sides of the equation, we get
\[\begin{array}{l} \Rightarrow 2\angle OAB + 60^\circ - 60^\circ = 180^\circ - 60^\circ \\ \Rightarrow 2\angle OAB = 120^\circ \end{array}\]
Dividing both sides by 2, we get
\[ \Rightarrow \angle OAB = 60^\circ \]
Thus, we get
\[\angle OAB = \angle OBA = 60^\circ \]
We can observe that in triangle AOB, we have \[\angle OAB = \angle OBA = \angle AOB = 60^\circ \].
Therefore, the triangle AOB is an equilateral triangle.
We know that all the sides of an equilateral triangle are equal.
Therefore, we get
\[AO = BO = AB = R\]
Now, OP is the radius joining the tangent of the circle AB at the point of contact.
Therefore, the angle \[OPA\] is a right angle.
Thus, OP is the altitude of the triangle AOB.
The altitude of an equilateral triangle is also a median of the triangle.
This means that it bisects the side into two equal parts.
Therefore, OP bisects AB, that is
\[AP = BP = \dfrac{{AB}}{2}\]
Since \[AO = BO = AB = R\], we get
\[AP = BP = \dfrac{R}{2}\]
Finally, we will find the required ratio using the Pythagoras’s theorem.
The Pythagoras’s theorem states that the square of the hypotenuse of a right angled triangle is equal to the sum of squares of the other two sides, that is \[{\rm{Hypotenuse}}{{\rm{e}}^2} = {\rm{Bas}}{{\rm{e}}^2} + {\rm{Perpendicular}}{{\rm{r}}^2}\].
Therefore, in triangle APO, we get
\[A{O^2} = A{P^2} + O{P^2}\]
Substituting \[AO = R\], \[AP = \dfrac{R}{2}\], and \[OP = r\] in the equation, we get
\[ \Rightarrow {R^2} = {\left( {\dfrac{R}{2}} \right)^2} + {r^2}\]
Simplifying the expression, we get
\[ \Rightarrow {R^2} = \dfrac{{{R^2}}}{4} + {r^2}\]
Subtracting \[\dfrac{{{R^2}}}{4}\] from both sides, we get
\[\begin{array}{l} \Rightarrow {R^2} - \dfrac{{{R^2}}}{4} = \dfrac{{{R^2}}}{4} + {r^2} - \dfrac{{{R^2}}}{4}\\ \Rightarrow \dfrac{{4{R^2} - {R^2}}}{4} = {r^2}\\ \Rightarrow \dfrac{{3{R^2}}}{4} = {r^2}\end{array}\]
Multiplying both sides by \[\dfrac{4}{3}\], we get
\[\begin{array}{l} \Rightarrow \dfrac{{3{R^2}}}{4} \times \dfrac{4}{3} = {r^2} \times \dfrac{4}{3}\\ \Rightarrow {R^2} = \dfrac{4}{3}{r^2}\end{array}\]
Dividing both sides by \[{r^2}\], we get
\[ \Rightarrow \dfrac{{{R^2}}}{{{r^2}}} = \dfrac{4}{3}\]
Rewriting the expression, we get
\[ \Rightarrow {\left( {\dfrac{R}{r}} \right)^2} = \dfrac{4}{3}\]
Taking the square roots on both the sides, we get
\[ \Rightarrow \dfrac{R}{r} = \sqrt {\dfrac{4}{3}} \]
Simplifying the expression, we get
\[ \Rightarrow \dfrac{R}{r} = \dfrac{2}{{\sqrt 3 }}\]
Therefore, we get the ratio of the radius of the circumscribed circle to the radius of the inscribed circle as \[\dfrac{2}{{\sqrt 3 }}\].

Thus, the correct option is option (d).

Note:
We used the S.S.S. congruence criterion, and the angle sum property in the solution.
According to the S.S.S. congruence criterion, if the corresponding sides of two triangles are equal, then the two triangles are congruent.
According to the angle sum property of a triangle, the sum of all the interior angles of a triangle is always \[180^\circ \].